超難問
等間隔で正方形状に並んだ9個の点。
すべての点を通るように4本の「連続する」直線を引いてみてください。
（連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です）
答えにたどり着くには柔軟で自由な発想が必要。
解けたら天才…かも
解けなかった方は下記の解答ビデオを御覧ください。
266 件のコメント
コメントするには、ログインまたはメンバー登録（無料）が必要です。
等間隔で正方形状に並んだ9個の点。
すべての点を通るように4本の「連続する」直線を引いてみてください。
（連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です）
答えにたどり着くには柔軟で自由な発想が必要。
解けたら天才…かも
解けなかった方は下記の解答ビデオを御覧ください。
そこまで楽しんで頂けると投稿者冥利に尽きます。😁
あはは、私もそれ考えました。
M字ですよね。
でも、一応点や線に大きさは無いというお約束で…
>歴史は繰り返されるのですね
何やら意味深なような、そうでもないような…
将来は「0本」という回答が発案されることでしょう。
おお、お友達発見。👍
「0本」の次はいよいよマイナスの世界ですね。（笑）
と言えるなら‥‥と
私はその辺で降参して
動画を見て実感できました。
ヤッパリ 私は馬鹿だと。
太い筆を使う案は、ガキのたわごとではなく、一つの基本的な考えなのですね。
それなら、もう少しかっこいい書き方をしなければなりませんね。ということで、以下のように言い換えておきます。
平面上の複数の任意の点は太い1本の直線上にある（おとぶの定理 : ｳｿ）。
出題画像にあるオレンジのマーカーを使わない（筆？太い!?）
という発送は思いつかなかったです('ω'*)
（正直に言うとマーカーを破壊するイメージはして、止めましたｗ）
出題文の（＞直線を引いてみてください。）を
無視していいなら、0本「1点」ですよね。
多分、分かった人の8割は過去の記憶ですよ。
ちなみに私は過去にやった気がするけど憶えてない…😭
>太い1本の直線
それって長方形ですよ（笑）
Dセットさん
>0本「1点」ですよね。
そうなるともう円ですよ（笑）
くっついてなくて良いなら、昔やったので分かるんだけど…。
>連続しない4本の線って
「連続する」です。
>4本目の終点は他の3本とくっついてなくていいの？
オッケーです。
>昔やったので分かるんだけど
良い記憶力ですね。
素晴らしい。
👏👏👏
『その方向展開する位置が正しいこと』を証明するため、
事前に補助線を引いたり、紙を前提として折り目をつけることは、ルールに反しないのでしょうか？
本件とは無関係ですが、角を三等分する際に、折り目を付ける発想は、すごいなと思いました。
さらに言えば、『その方向展開する位置が正しいこと』を証明しなくても良いような気すらします。（笑）
9個の黒点すべてを一度だけ通過するように
4本の「連続する」直線を引いてみよぉ～で
（たぶん出題者の期待する）正解にたどり着きました♪
Darkさん楽しかったです。
後で動画見ますね（見ました）
…ほぼ、あってました('ω'*)
>…ほぼ、あってました('ω'*)ほぼってことは、このくらいは違うのね？
問題用紙や解答用紙を折ったり切ったりしてはいけません。
って書いてあるところ。
だから補助線はいいかなと思いまして〜
＞ほぼってことは、このくらいは違うのね？どちらもほぼほぼですが、アゴとか微妙ぉ～に違っていて
こちらが正解みたい(｡･ω･｡)
「柔軟で自由な発想」がヒントになってますね(o^^o)
幾何数学の証明では、補助線やらコンパスの円弧やら描くのは使うので問題ないですよね
私は脳内でしかやってないので不正確な作図にはなりませんが・・(^^)
まあ、相手が紙なら折りたたんで重ねた点にエンピツ刺せば一本ですけどね
最初解らんかったけど、今見たらできました。(^O^)/
解けました
でも
閃いたんじゃなくて 思い出しただけでした⤵
(=_=)
同じく
似たような問題を知ってました
閃いた人も思い出した人も大したもんです。
👏👏👏👏👏
黒点が「始点・終点である」という制限がないのがミソですね！
動画は今確認して正解でした＼(^o^)／
子供の頃に書いたアノ形です❤
このコメントに今気が付きました。
>相手が紙なら折りたたんで重ねた点にエンピツ刺せば一本ですけどね
確かに、綺麗に折りたためば点は重なりますね。👍
👏👏👏
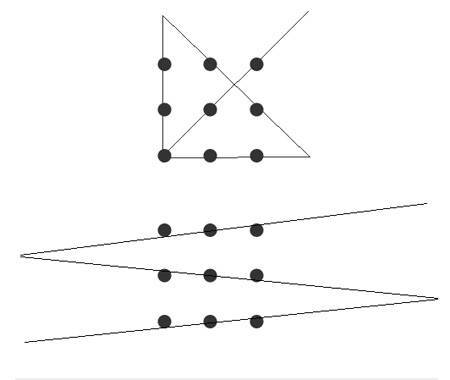
ウエブで見たんですが。これって正解ですか？これじゃ詐欺だろうよ(笑)。
因みに､私出来ませんでした(悲)。
10分考えたけど諦めました
線を長く延ばしてまでは想像したけれど
情けない～
上段が正解です。
下段は点に見立てた小さな円を小さくすれば分かりますが、横線が3本とも平行でないと横並びの3点を通らないので不正解です。
> 思い出した人も大したもんです。
思い出して解けても良かったんですね
良かった良かった
答えはビデオの中にありますので、どうぞご確認下さい。
てんがろんさん
解説有難うございます。
この手の用語のお約束として、点や線に大きさ（面積）は無いということになっています。
norinori7さん
おお、またもお友達発見。😁
私の場合は、下の4分類で④でした…😭
①天才（解答が閃いた人）
②秀才（過去の記憶で解けた人）
③普通の人（初めてで解けなかった人）
④ボケ老人（過去の記憶すら思い出せなかった人）
本当の超難問をお願いします！
👆この手のコメントに何と返して良いものか…まず、ぱっと見て、「普通」にやろうとしたら詰むんだろうなあ、と予測。
そして、「普通」の枠内で線を引いたのでは無理である事を確認。
それでは、自分が縛られてる枠を外さないと駄目だから…と切り替えて考えてみたら、すぐに答えがわかりました。
どうせ何かあるんだろう、と最初から他の可能性を探ってたからか、ハマる事なく一発でした。
これ、ちょっと図形の証明問題とか思い出しますね。
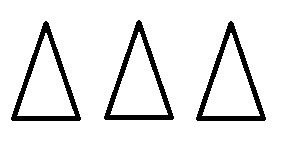
皆さん頭が柔らかいですね。では、この問題も楽勝でしょう。
問題：上図のような二等辺三角形をしたケーキを4人で均等に分けるには、最低でも何回切る必要があるでしょうか？
１回。
でもケーキって、形も楽しむものじゃないのかな。
マイネ神さんちょっと何言ってるかわかんないんですけど…
ほぼ正解ですが、もう少し綺麗に切りたいですね。
ケチんぼーー！
( `Д´)ﾉ