JavaScriptを有効にしてお使いください
JavaScriptの設定方法はこちらの検索結果を参考にしてください
等間隔で正方形状に並んだ9個の点。すべての点を通るように4本の「連続する」直線を引いてみてください。(連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です)答えにたどり着くには柔軟で自由な発想が必要。解けたら天才…かも解けなかった方は下記の解答ビデオを御覧ください。
メンバーがいません。
直角二等辺三角形の斜辺を底辺とすると、高さは底辺の半分やから(合同な2つの直角二等辺三角形ができる)
ではあきませんか?
ninnin80sさん
大正解です。
皆さん思考が大変スマートですね。
では、問題を修正させて頂きます。【問題】
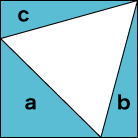
次の図ように正方形に1辺10cmの正三角形が内接しています。
a〜cの着色部分の合計面積を「作図によって」求めなさい。
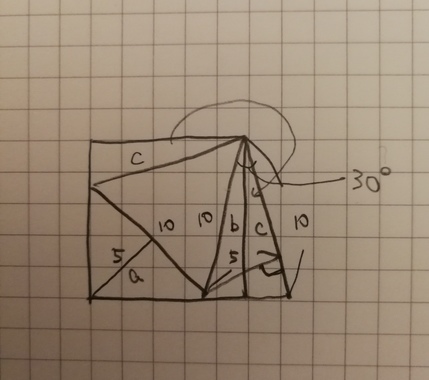
10x5/2x2=5050cm2
ですかね。
右の三角形「b+c」の高さ「5」はどうやって求めたのでしょうか?
一つにまとめないとあかんのかと思ってました^^;
(2つくっつければ正三角形)
また帰ってきて続いているようならみなさん遊んでください~
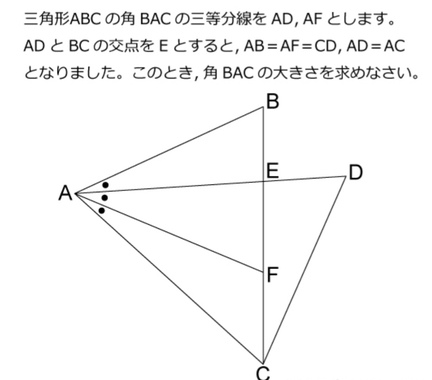
問題に、角度の数値が一つもないものです。図がわざと変に書いてあるので、注意してください。
難易度は相当高いはずなので、ヒントを。
補助線はいりません。
解説ありがとうございます。
着いていけない~(苦笑)
眺めるだけで、参加には二の足を踏んでます💦
と書いたのは、算数オリンピックファイナルの問題だからです。補助線10本くらい当然のように引くという世界の話なんですが、これは辺や角の同じところに印をつけていけば、そのうちできると思います。
算オリファイナルの中では簡単なレベルですので、是非トライを。
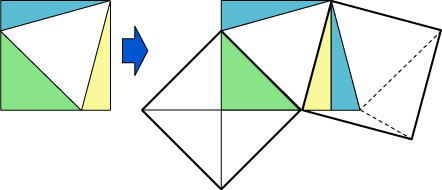
>30° 60° 90°の直角三角形では斜辺と短辺の長さは2:1ですよね~なるほど、その知識を使うと簡単ですね。
ちなみに、面倒ですが全て図形で解くと上図のようになります。
図形より、どちらも一辺10cmの正方形の1/4となり、足すと1/2の50cm2と出てきます。
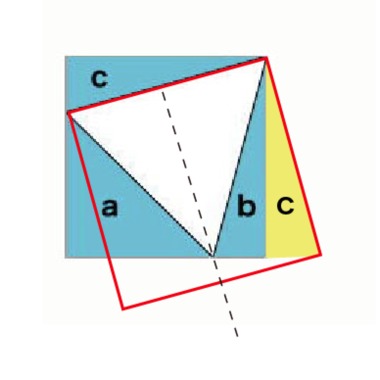
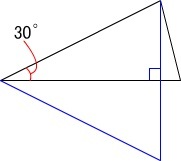
右の三角形の高さを求めるだけなら、この図のほうが簡単ですね。67.5°ですね。
(ただし、補助線を一本だけ引きました)
>200-10√300
10cm角の正方形と勘違いしてた・・・
寝ぼけてたんだなあ(^^)
答えを出してから整理したら、補助線なしでいけました。👍
お疲れ様でした。m(_ _)m
はい、私も正方形が10cmと読み間違えて一生懸命計算して
改めて読んだら三角形が10cmなので、面積を出すのは簡単じゃんとなりました
気付いた後も、aの一辺が5√2だから面積が25cm2というのはすぐに出たが
10cmを底辺とした時の高さが5cmになるところまでは気付けませんでした
10cmの正方形から直角三角形の一辺を求めようとしたために
その辺に目が行ってしまったのもあるのでしょうけど
解けましたか。これで算数オリンピックも大丈夫ですね。
この問題、私は算数オリンピックファイナルの問題という情報だけで解いたのですが、図形を移動したり、補助線を引きまくったりして20分くらいかかりました。あとから見ると、引いた補助線を使ってないという。一つも情報が無いほうが解きやすいかもしれません。
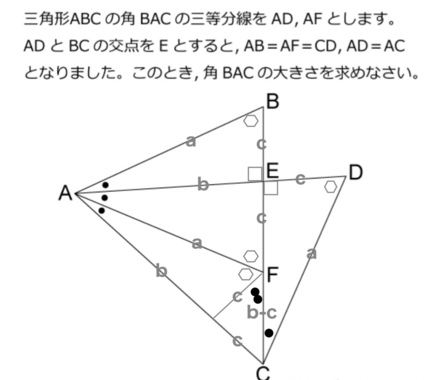
最初はこんな感じで点Fから線分ACへ垂線を下ろし、直角二等辺三角形を作って角度を追い込んでいきましたが、見直したらもともとの図形に良い感じの直角二等辺三角形があることに気が付きました。こういう問題って良いですね。
凄く前のコメントですが、宛名を間違えておとぶさんと書いていました。
ごめんなさい
https://king.mineo.jp/my/132c3b2f477438a4/reports/45637/comments/1386144
あと名前もずっと「n」と「m」を間違えて書いていました。ごめんなさい。
<m(__)m>
あ、私も全く気付いてなかったです。勝手に自分宛てだと思い込んでいました(内容から)
ハンドルも気づきませんでしたよん(老眼か^^;)
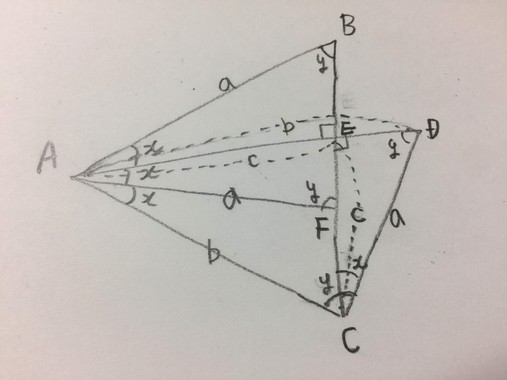
Dさんの答えを見ずに自力で解けました~気付けば簡単なのに、なかなか気づかなかったよ(笑)
●三角形AFBは、2辺が同じ長さaで、二等辺三角形。
したがって、角AEBは直角。
●三角形ACDも、2辺が同じ長さbで、二等辺三角形。
三角形AFBと三角形ACDは3つの角が同じ相似形。
したがって、角度yは同じ。
●三角形CEDは、三角形AEBと合同。
2角と1辺の長さが同じだから。
したがって辺AEと辺CEは同じ長さc。
●三角形EACは直角二等辺三角形。
したがって、角度2x=45度
答え 67.5度
おみごとです。
算数オリンピック金メダルも夢じゃなさそうです。
そういえば、宛名のとこ、何か違ってましたね。すっかり忘れてました。(老眼ならぬ、ボケが始まったか)
これだと補助線が不要になり、シンプルだと思います。👍
Dさんの問題、bcの三角の面積を出す方法、全くわかりませんでした。https://king.mineo.jp/my/132c3b2f477438a4/reports/45637/comments/1386327
ググったら載ってました。
http://www.vimagic.co.jp/sansu4/gokui/130131/1-31.html
「夾角30度の二等辺三角形の場合、等しい変の長さが10cmなら、
正三角形を利用することで、
高さは斜辺の半分になり5cmですから、
面積=10×5÷2=25c㎡ になります。」
うわーこんなの思いつかない。慣れなのかひらめきなのか。
そうです。
そのページから問題をお借りしました。
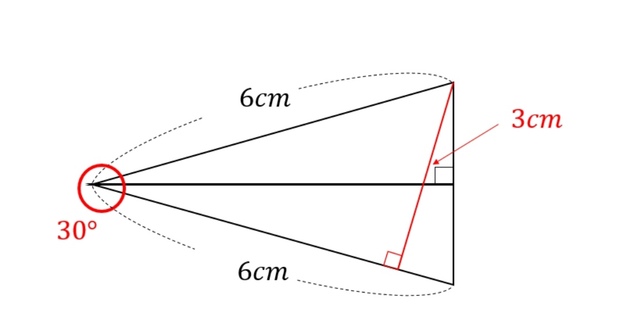
これは、中学入試受験塾だと、4,5年で覚えさせられますので、慣れですね。ひらめく人もいるかもしれませんが。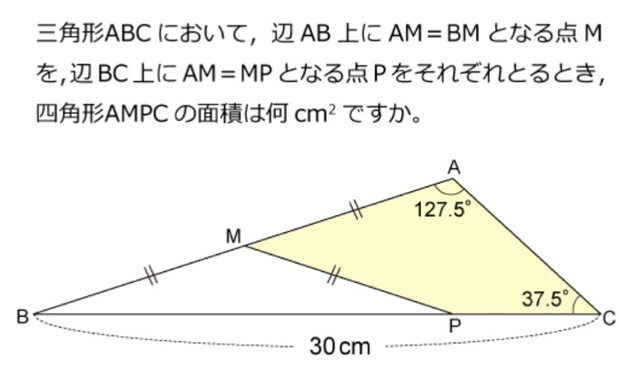
応用です。上と同じ形にもっていってください。
上と同じ形にするのに、補助線2本。
そのあと、黄色の部分を求めるのに、補助線3本です。
56.25c㎡ですね。
これは良問だと思います。👍
素晴らしいです!!
算数の難問って、どうやって基本パターンに当てはめるかなんですが、127.5度を見ると嫌な予感しかしません。
ジュニア算数オリンピック ファイナルの問題なのですが、その中でも難しい方に入ると思います。
いや~おめでとうございます。
しかし、ヒントがあったから、37.5°が75°の1/2だということに気づけたので、自力では多分解けなかったでしょう。
4つの三角形の2ペアが面積同じ、とわかっていたのにもかかわらず、解けないって~
我慢できず、答えをググってしまいました。
いやあ本当に何故ひらめかないんだろう~
これはスレタイ通りの超難問ですので。補助線を図形の外に引くのはふつう躊躇してしまうものです。最初の9個の点の問題も同じですね。
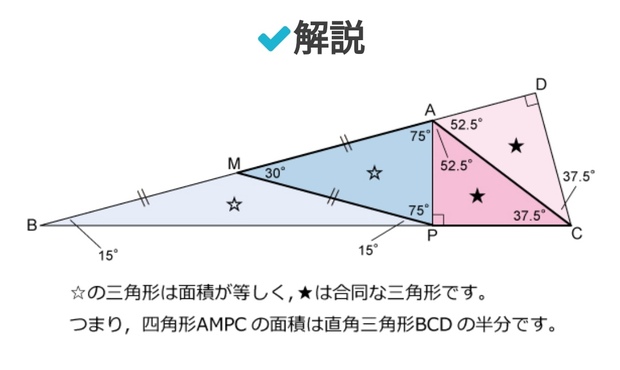
解答です。まず、三角形ABCの内角から角B=180-127.5-37.5=15。
これで1角が15度、1辺が30cmの三角形ができました。
15度の三角形の面積を求めるパターンにするため、30cmの辺を斜辺にする直角三角形を作ります。
CからBAの延長線上に垂線を下ろしその足をDとすると、1角が15度、1辺が30cmの直角三角形より、三角形BCD=30x15/2/2=112.5
後は、上図の星印のとおりで、半分にして、
56.25c㎡になります。
考えていただいた皆さん、お疲れ様でした。
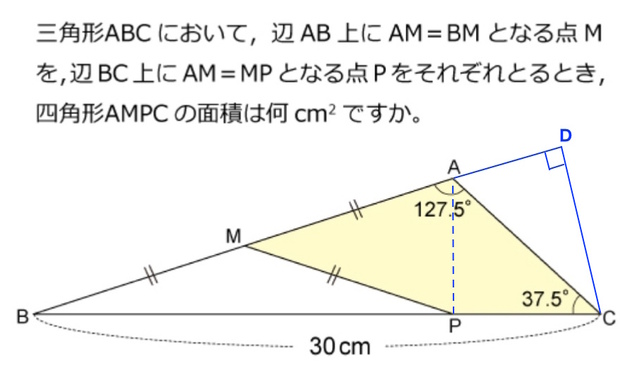
おとぶさんおはようございます。
最終的には解説の通りに解けたのですが、図形が(わざと)いびつに書かれているため、線分ADが線分APよりかなり短く見え、この二つの三角形が合同であることに気付くのに時間がかかりました。
拾ってきた解答の図は、全体を書き直してあるんですね。
算オリとか難関中学・高校の入試問題は、与えられた図面が正確ではないのはデフォルトですので。
ちなみにやり方が思いつかない場合は、図を自分で書き直してみるということも私はすることがあります。というか、たいてい自分で手書きで書いています。ひとつ前の算オリの角度の問題は書き直して2直線が直交することが分かりました。
この問題はどうしたかな?最初に解いたのは結構前で印象に残っていたから、多分手書きしたんじゃないかな。
というか、書く気が全く起きないんですけど〜(笑)

お、これは良いかも、と思ってコピーしましたが、超簡単でした。😫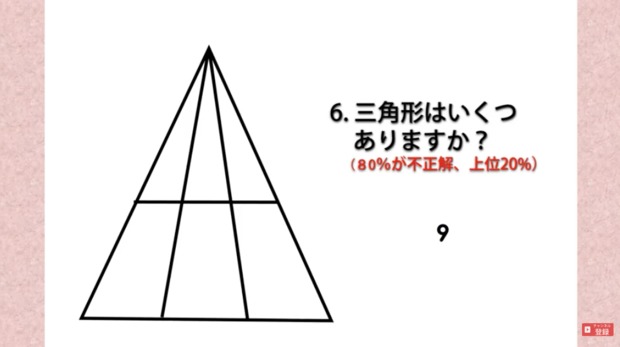
こっちのほうが難しいかも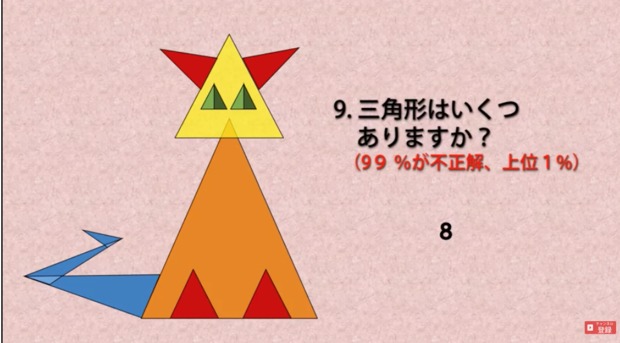
もう一つおまけなんかちょっと安心しちゃいました^^;
ありがと〜
付き合ってくれるのはみさとちゃんだけだよ〜〜😭
こんな掛け算の解き方があったとは〜〜❗❓
みさとちゃんも学校で自慢してみよう!