超難問
等間隔で正方形状に並んだ9個の点。
すべての点を通るように4本の「連続する」直線を引いてみてください。
（連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です）
答えにたどり着くには柔軟で自由な発想が必要。
解けたら天才…かも
解けなかった方は下記の解答ビデオを御覧ください。
266 件のコメント
コメントするには、ログインまたはメンバー登録（無料）が必要です。
等間隔で正方形状に並んだ9個の点。
すべての点を通るように4本の「連続する」直線を引いてみてください。
（連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です）
答えにたどり着くには柔軟で自由な発想が必要。
解けたら天才…かも
解けなかった方は下記の解答ビデオを御覧ください。
15度は違いました！はずかしー
すぐ直したいけど、もうベッドの中なので、明日直します。
私の図、一部間違っています。ごめんなさい。
>>それって、「インターステラー」のワンシーンでしたね。
>えっ、それはアルキメデス・・・・
アルキメデスが叫んだ言葉として有名ですが、映画「インターステラー」の最後のほうで、主人公の娘がブラックホールの謎を解く数式を発見した際に、「エウレカ」って叫んで計算用紙をバ〜〜っと研究室にバラ撒くシーンが印象的でしたので、つい…
真ん中に正三角形をおいて、DSoMさんの色分けの三角形が同じ図形となるわけですね
あとは面積で、1=2、2=7、同、3=4、5=6となるのか
そういや学校出てから幾何学は実生活で使ってないなあ
BCをa:bに分ける点Dをとり、AとDをむすぶ。
CAをa:bに分ける点Eをとり、BとEをむすぶ。
ABをa:bに分ける点Fをとり、CとFをむすぶ。
とすると、中に出来る三角形が、正三角形になることは分かると思います。
後は、a:bを適当に決めたら、BPがAPの2倍になった。そのあと線をいくつか消した。
という感じです。
なお、a:bを求めるのは、ベクトルあたりを使うことになるのでは？
手元に紙がないので、言葉だけですみません。
pmakerさんはわかったんだ。イマイチなのは、私だけ？
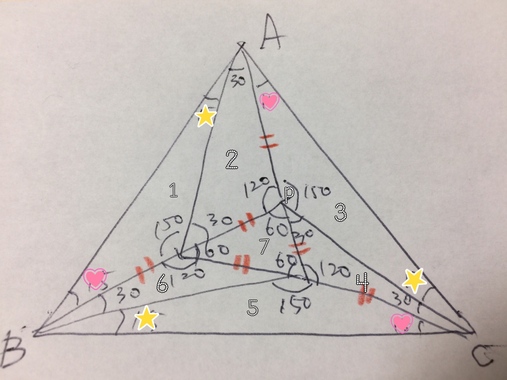
まずは正三角形を置いてみる。
あるいは、Dさんのように並べてみる。
すると結果こうなって7つの三角は同じ面積になる
という解き方なんですかね？
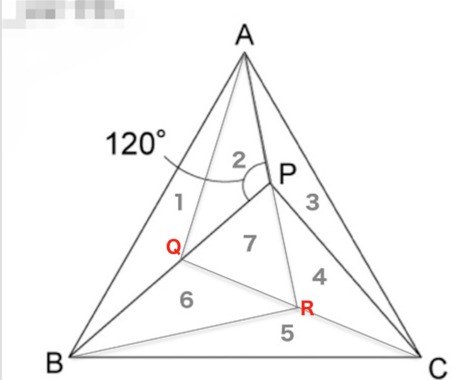
私がお風呂で閃いた手順は下記です。①BPの中点QとAを結ぶと△ABQと△APCは合同となる（2辺とそれが挟む角度が同じ）
②△ABQと△AQPの面積は同じ（底辺の長さと高さが同じ）
③次に、点QとCを結ぶと△QBCと△ABPは合同となる（2辺とそれが挟む角度が同じ）
④同様に点RとAを結ぶと△QBCと△ARCは合同となり点Pを通る（角PACと角RACが同じ）
⑤以上より中央に残された△PQR以外の面積は△APCの6倍となる
⑥また、△PQRは△BQRと面積が同じ（底辺と高さが同じ）
⑦以上より、△ABCの面積は△APCの7倍
参考になれば
①の挟む角度が同じ、というのがなぜなのか…
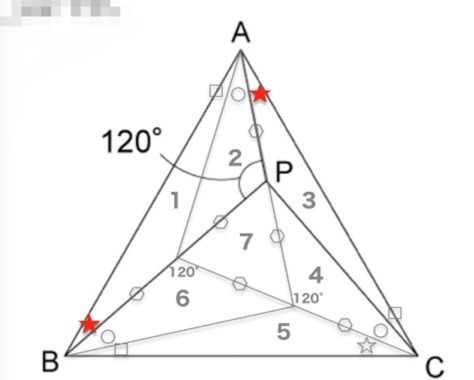
さとさん>①の挟む角度が同じ、というのがなぜなのか…
角PACは60°から角PABを引いたもの
角ABPも60°から角PABを引いたもの
故に同角度
です。
なるほど
内角の和180-120-角PAB＝角ABP
ですね
で、その時に☆の角度を求めても良いのですが、その分時間がとられますので、☆のままで作業を進めた方が早く正解に辿り着けると思います。
だから120度の場合に、重ならずにぴったりとパズルのように並ぶ、と。
120度は360度のちょうど1/3ですからね。
回転させれば解けるというヒントだと思いました。
回転させれば解けるというヒントだと思いました。
こう言われると、またわからんよ💧
真ん中からズレた120度と、回転が全く結びつかない
120度の位置がズレてるから、回転出来るのか出来ないのか、よくわからなくなってしまうと。
お仲間♪
一緒にするなと言われそう〜（笑）
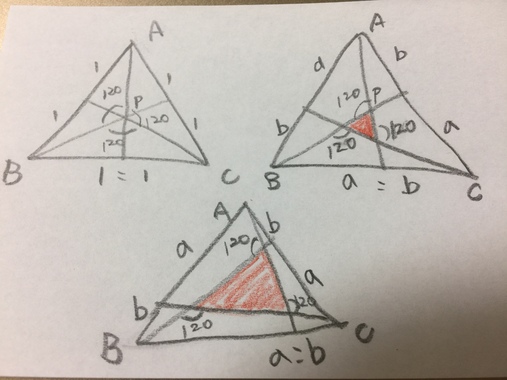
おとぶさんの補助線の話は、最初に真ん中に正三角形を作る。
a:bの比率を色々調整していたら、その内にBPがAPの2倍になった。
だから、風車のように回転できる形なのは当たり前。
という事ですね。
Dさんが120度は回転出来るヒントと書いていたのと同じ事ですね。
うわー、自分の頭の悪さ固さに改めて驚く～
というか、皆さんの頭良すぎ〜
ついでですので線分の比率を求めてみました。久しぶりにベクトルを使ったので、間違ってるかも。高校2年レベルの数学の知識が必要。
正三角形の各辺を、a:b=2:1に分けるといいみたいです。
私にはベクトルの計算全くわからないのですが（ごめんなさい💧）
a:b=2:1
なのであれば、角PACは20度になるんですね。
角PABは40度、
角QABは10度
なんですね。
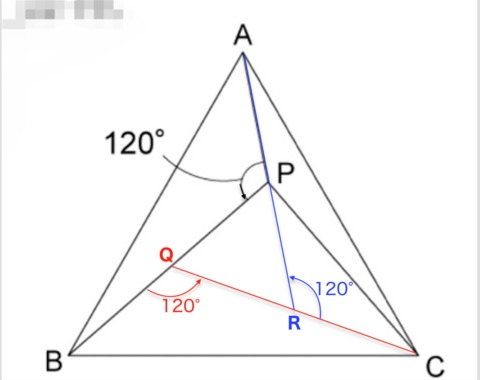
さとさん>こう言われると、またわからんよ💧
失礼しました。
上図のように、線分APを120°回転させた位置に線分BPがあるということは、三角形APBを120°回転させた三角形BQCは線分BPに重なり、そこからさらに120°回転させた三角形CPAも、線分QCや線分APと重なり、隙間なく回転させることができる、という意味でした。
中学生レベルだとこんな感じ？走り書きなんで汚くてすいません^^;
おおー私にも理解できました。
ATに平行なQSを引けば、図で簡単にわかる♪
すばらしい～
回転軸を、ど真ん中から徐々にズラしていく、という事が、おとぶさんの補助線の話で、わかりました。（最初から気付くのは凄いと思う）
https://king.mineo.jp/my/132c3b2f477438a4/reports/45637/comments/1385003
>回転軸を、ど真ん中から徐々にズラしていく…
いや、そんな高度な発想ではなく、三角形の3辺に沿って回転させただけです。（笑）
そのおかげで、小学生並みの柔軟な発想ができたのかも（笑）
おそらくメネラウスの定理あたりでもいけると思うのですが、うる覚えで公式を確認するのがめんどくさかったのと、公式だと味気ないと思ったので（笑）
いやぁ、わかりやすい。
これをマイネ王標準解と定めておきましょう（笑）
深みのある良問をありがとうございました。
まだまだ沢山お持ちのようですよね？
また計算のいらないやつを一つお願いします。
＞いや、そんな高度な発想ではなく、三角形の3辺に沿って回転させただけです。（笑）
120度×3=360度だから３回転できる、と直感で思い付くのは、
私の頭ではPQRがほぼ１点に集中している場合だけだったんですよね。
PQRが離れていても回転させたらピッタリ合う、と思い付く人は凄いと思うけど、私の頭では無理だっただけの話です。
辺に沿って角度を変えると「ピッタリ合う」事を理解するには、
私の頭では「角ABPと角PACは同じ角度」という情報が必要でした。
あくまで私の頭で「直感で」わかる範囲の話なので、もっと少ない情報でわかる人は凄いと思うんだけど。
＞おそらくメネラウスの定理あたりでもいけると思うのですが、
ググってみました！
http://www.mathlion.jp/article/ar019.html
証明見てなるほどと思ったけど、こんな定理覚えられん(笑)
それにしても、皆さん凄いですね。
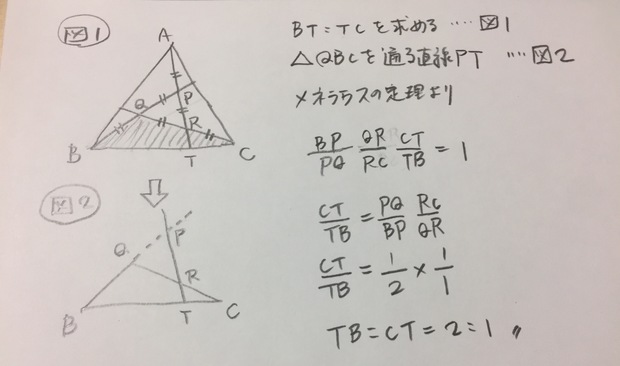
おとぶさんとminmin80sさんが解いていた、a:b(上図のBT:TC)を求める問題。
教えてもらったメネラウスの定理で解いてみた。
たぶん、5分後にはこの定理忘れてると思う（笑）。
https://king.mineo.jp/my/132c3b2f477438a4/reports/45637/comments/1385076
直線PTと平行な直線QSを引いたら、この定理になりますね！
素晴らしい。聞きかじったメネラウスを使ってで解いてしまうとは^^
まさにそうなんです。補助線無しで比を求めようと公式化されたものがメネラウスの定理なんですね。
そこまで考察されるとはあっぱれです〜
こっちに平行線書く証明が載ってたので、そのままですよ。
http://www.mathlion.jp/article/ar019.html
私が自分でイチから考察して気付くわけがない（笑）
http://sansu-seijin.jp/?p=14931
https://twitter.com/sansu_sommelier/status/1086519195389423616
私の手順で大体あっていたようです。
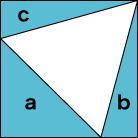
ネットで拾った（多分有名な）問題ですが、いかがでしょう？【問題】
次の図ように正方形に1辺10cmの正三角形が内接しています。
aの部分の面積を求めなさい。
10×10÷4=25
答え 25cm^2
ではない？
電卓使わないと出ない答えなので違うでしょうね ┐(´д｀)┌
右の図計の問題の時のように引っかかって、一生懸命計算していました
その答えの根拠が一目でわかる図で表現してみて下さい。
図計→図形
>電卓使わないと出ない答えな
>ので違うでしょうね
はい。
さとさんの25cm2が正解になります。
>一生懸命計算していました
有り難うございます。
出題者としては嬉しい限りです。
(10/√2)×(10/√2)÷2=25
△cと△bは直角三角形なので、斜辺と他の一辺相等で△c≡△bです。
なので、△aは直角二等辺三角形です。
△aから正方形の対角線を引けば、一辺5の正方形の面積と同じですね。
わざわざ△aの二等辺を求める必要はありませんでした。