小学3年の算数の宿題、この解き方なんか変じゃない？（夏休み編）

前回のスレが楽しかったので、またまた小学校の算数についてのスレです。
https://king.mineo.jp/my/sato/reports/37290

子供の夏休みの宿題で、こんなのがありました。

●問題１：
まりあさんの組は２７人です。はんを６つ作ります。４人のはんと５人のはんがそれぞれいくつできるでしょう。

■問題１の旦那の解き方：
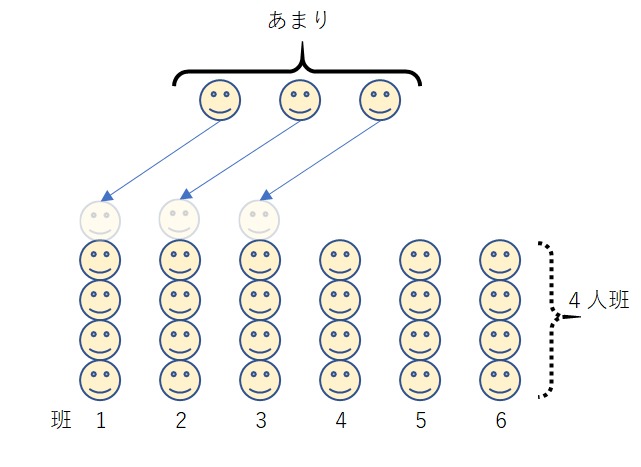
27÷6=4あまり3 → 全て4人班だとすると3人余る → 5人班が3つ。
6-3=3 → 5人班が3つだから残り3つが4人班

いやあ、確かに上図の通り、その答え方を出題者は求めているのだと思います。割り算の文章題ですからね。

でも、どうも納得が行かない私。
たまたま４人班と５人班だから解けたけれど、これの人数が異なる場合、同じ解き方では解けませんよね。例えば...

●問題X：
「まりあさんの組は３０人です。はんを６つ作ります。４人のはんと７人のはんがそれぞれいくつできるでしょう。」

■問題Xを旦那方式で解くと、
30÷6=5あまり0
「え？5人の班じゃないから」となります。
30÷4=7あまり2
「え？7つも班が出来たら困る」となります。

という訳で私の解き方

■問題１の私の解き方
aを4人班の数、bを5人班の数とします。
　4a+5b=27
　a+b=6
の連立方程式で、答え a=3,b=3

つまり、これを小学生でもわかる解き方に変えると、
　4×6=24　　←全て4人班の場合
　27-24=3　　←3人余る＝5人班は3つ
　6-3=3　　　←残り3つが4人班
答え：4人班が3つ、5人班が3つ

これなら、人数が変わっても解けます。


■問題Xの私の解き方
　4×6=24　←全て4人班の場合
　30-24=6　←6人余る
　7-4=3　　←7人班と4人班の差は3人
　6÷3=2　←余り6人を3人ずつ2班に配れる＝7人班は2つ
　6-2=4　←残り4つが4人班
答え：4人班が4つ、7人班が2つ



いやいや、わかっています。
この問題１には、次の前提が含まれている事を。
まりあさんの組の人を「できるだけ均等になるように」6班に分けるんですよね。常識的に「均等」に決まってるから、問題Xのように4人班と7人班なんてあり得ないから！って事だと思います。均等に分けるから割り算で解けるんだよ、って事だと思います。

だけど、どうも納得が行かない問題だと思いませんか？


→2018/8/20追記：
おとぶさんによると、問題Xのようなのは、つるかめ算の典型的な問題だそうです。つるかめ算の解き方は、私の解き方のように、全てどちらかだった場合、と仮定して計算するみたいですね！

な、なんと答えがわかりました。
というか、先生の回答もミスありです（！？）

元々、親子で答え合わせをするように、回答集を貰っているのですが、この文章題のページだけ抜けていたんです。わざと抜いてあるのかと思ったら、他のお友達にはこの問題の回答が付いていたそうです。
写真を送って貰いました。

えっ！
答え：4人の班が4つ、5人の班が3つ
って先生答え間違えてるやん！　orz

でもまあ、式を見ると予想通り旦那方式で、余りの数を5人班としている事はわかりました。
そして、コメント欄で色々出ていた等分除なのか包含除なのか、は等分除(27÷6)が模範回答となっておりました。
それにしても、問題も変だし、先生の答えも変って、いったい何～！？
な宿題でした。