子供(小3)の算数の問題わかる?→答えがわかりました。
まーたくモバイルと関係無い話題ですみません。
小学校3年生の算数の宿題で、子供と私とで意見が分かれています。
皆さんはどう思われますか?
■問題:
『子どもが34人います。1つの長いすに4人ずつすわります。長いすはいくついりますか。』
■答え案1(私の考え):
34÷4=8 あまり2
答え:9つ
※理由は、子ども34人全員が座るには4人掛け×8つ、2人掛け×1つ、合計9つ必要。
■答え案2(子供の考え):
34÷4=8 あまり2
答え:8つ
※理由は、4人掛け長いすが8つ、長いすでは無い椅子に残り2人が座る。
問題に「4人ずつすわります」とあって、「4人まですわれる(2人でもOK)」とは書いていないから。
問題に「全員が長いすに座る」とは書いていないから。
※学校の先生に、「全員」「全て」といった言葉がある場合に、あまりを1として足す、と習ったらしい。
※追記です。
子供が言うには、残り2人は別の椅子に座るとは限らなくて、立ったままかも知れないし、別の部屋へ移動するかも知れないし、その2人がどうするかまで考える必要は無い、という事です。
とにかく長いすには4人「ずつ」座る、と書いてあるから、長いすは8つだという事です。
割り算のあまりをどう処理するか、という事を習ったばかりのようです。
余りの分も1として加算して答えるべき問題と、余りは除いた値を答える問題とが混在していて、文章から読み解く、という練習です。
例えば、
【問題A】
「おり紙が42まいあります。このおり紙を8まいずつたばにします。8まいずつのおり紙のたばは、いくつできますか」
→これは、余りを除いた数が答えですよね。
42÷8=5あまり2 答え:5たば
【問題B】
「本が28さつあります。この本を1回に5さつずつはこびます。全部はこび終わるには、何回はこべばよいですか。」
→これは、余りを1として足した数が答えですよね。
28÷5=5あまり3 答え:6回
【問題C】
「子どもが35人います。4人まですわることのできる長いすにすわっていきます。みんながすわるには、この長いすはいくつあればよいでしょうか」
→これは、余りを1として足した数が答えですよね。
35÷4=8あまり3 答え:9つ
さて、一番上の本題の「4人『ずつ』すわります」が、
問題Aの「8まい『ずつ』の束」と同じ種類の「ずつ」と考えるのか…
あるいは問題Cの「4人『まで』すわれます」と同じ種類と考えるのか…
7月18日15:30 やっとドリルの答えがわかりました!
答え:9つ
だそうです。
常識的に「子供は全員この長椅子に座る。余った人は4人未満で座ってもOK」という前提だったという事ですね。




でも、耳のほうが良いような気がしないでもない(3月3日は耳の日)
>GPS向けの衛星はかなりの高度を高速で飛んでいますので、
>地球上より時間が速く(でよかったかな)進みます。
残念ながら、逆ですね。
高速で移動する物体内の時間は、遅く進みます。
ちなみに、ISSにおける時間は、地球上の時間よりも6ヶ月につき0.007秒遅れるそうです。
◎→これだと②
の理由わかりましたよ
①は「これ」の次に「は」が付き、②だと「これ」の次に
「だと」が付き、③だと「これ」の次に「が」が付いています。
その差ですね?
ちなみにヒント♪
見たくない人は自由に!
ヒント1、常識に囚われてはこの問題絶対に解けない!
ヒント2、「+」
はい、ヒントをよく考えてね!
ヒント1は皆さんにも必要だと…
>◎→これだと②の理由わかりましたよ
大正解!頭柔らかいね👍
>ヒント2、「+」
分かった!💡、「8」か〜
結構難しいかも。
やっぱり逆でしたか。うーん難しい。システム屋さんにはよくわからんです。
いや、専門はバケ(金属)のほうですが。
理論を使う側にとっては、特殊相対性理論の式は簡単でいいですね。
物理の理論の方々、頑張って式を簡単にしてくださいね。
核反応による熱を計算して、物質の脆化を推定するとかで苦しんだ記憶が。
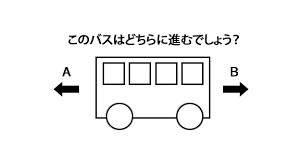
みさとちゃん、この問題分かるかな。(全然算数じゃないけど)
「(↑)このバスはどちらに進むでしょうか?」
ヒントは、日本の私立小学校の入試問題です。
Dさん、そのバスはどっちにも進みます!
それから8は不正解!もっとそんな常識吹きとばせ!+を使え!図形な…あ、これ答えにつながるわ
3+3= サンタさん
かな
後おとぶさん正解
ボーナス問題(解かなくてもよし)
ボーナス1、9+9+4+8=?
2、6+9=?
3、2+9=?
4、8+8=?
5、1+9=?
そのバス、B方向に進む?
(みさとさんと同じ答えですが)
以前何かで読んだ答えのドアの有無のヒントを、みさとに与えてしまいましたが。
右向き(ドアの有無)
https://rocketnews24.com/2016/02/12/707091/2/
左向き(運転手の姿が見えないから)
https://builder.japan.zdnet.com/blog/10514442/2009/05/29/entry_27022677/
トッチンさん
はい、B方向に進むで正解です。
ちなみに、イギリスでもB方向ですが、アメリカではA方向です。
もうお分りだと思いますが、重要なバスのパーツが一つ描かれていないために、運転席が手前右にあると類推する問題でした。
皆さん、慶應幼稚舎(少学校のこと)に入れるかも(笑)
サンタさんでしたか!!
よくあんないい加減なヒントでわかりましたね(笑)
素晴らしい。
👏👏👏👏

そっか。ドア方向で判断するのか?
俺はお尻の長さで判断してた。
Dさんの図をみるとタイヤの位置が非対称で、向かって右側の方がタイヤからバンパーまでが近い。
大抵のバスは前輪の方がバンパーまで近くて、後輪はバンパーから離れていてお尻が長いんだよね。
(後輪駆動でエンジンが後ろにあるから、構造的に後輪の位置がこうなるんだと想像しているんだけど)

トッチンさん>後輪はバンパーから離れていてお尻が長いんだよね。
上図のように、前のほうが長いバスもあるようなので、そんな微妙な違いを回答のポイントにしちゃうと親からクレームがつきそうですよね。
いやあ、運転手は描くべきだけどドアは描かなくても良い、という発想は不自然な気がします。
ドアは描くべきだけど運転手までは描かなくても良い、とか、ガラスで反射して中は見えない、という発想のほうが素直だと思います。
少なくとも、「運転手がいないから左向き」という回答を示された時、「ドアが無いから右向き」と回答した受験生(の親)から、「そんなの反射して見えないだろ」「室内描くなら椅子や乗客はどうなるんだ?」「そもそも、左向きならドアが書かれてないことをどう説明するのか」と、クレームの嵐になるでしょうね(笑)
Dさん
>GPS向けの衛星はかなりの高度を高速で飛んでいますので、地球上より時間が速く(でよかったかな)進みます。その分を考慮して調整しています。
>ちなみに、ISSにおける時間は、地球上の時間よりも6ヶ月につき0.007秒遅れるそうです。
まじですか~!
相対性理論って、「楽しいと時間が早く過ぎる」程度の話だと思ってたわ(←そんなわけない)
とか言ってるけど、「時間が地球上より遅れる」の意味が今一つ理解できません~
WiKiには「時計が異なる時間を指す」と書いてあるので、本当に時間が遅くなるんですね!
パラレルワールドみたい~
ところで、昔頭の良い友人が「大きい物体は動きが遅い」と言っていたんですよね。理論的に証明されてるとかなんとか。
小さい模型のゴジラを普通に動かして、拡大して見せたら、動きが速すぎて大きく見えない、という映画の話で言っていました。
これも相対性理論の重力で時間が異なる事と関係あるのかな?
なので小さい蚊はピョンピョン跳ねることができますが,ゾウはゆっくりとしか動けません。
ゴジラのサイズになると、多分立つこともできないでしょう。
横から失礼します。
GPS向けの衛星は高速で飛ぶと、特殊相対性理論では時刻の進み方が遅れ
かなりの高度で飛ぶと一般相対理論では、重力場の影響が小さいので時刻の進み方が早くなるそうです。
GPSカーナビのしくみ
http://ocw.u-tokyo.ac.jp/lecture_files/11351/6/notes/ja/06katori20121115final.pdfより
📌先ほど画像を添付しましたが、著作権に抵触するので削除しました。
なるほど。
それと、同じ速度で動いていても、小さいと速く見え、大きいと遅く見えるというのもありますよね。友人が言っていたのは多分それのような気がして来た。相対性理論は関係無さそう…
>勝ちゃん
そうなんだ!
高速だと時間の進み方が遅れ、高度が高い(=重力弱い)と時間の進み方が速くなるんですね。うーん不思議な世界~。(リンク先は難しくてよくわからなかったけど)
そうか、特殊相対性理論だけで考えちゃダメなんですね。
なるほど、GPSの場合は、特殊相対論により「-8.4×10{-11乗}」だけおそくなり、一般相対論により「5.27× 10{-10乗}」だけ早くなるので、合計で「4.45 ×10{-10乗}」だけ早くなっているということですか…
http://maya.phys.kyushu-u.ac.jp/~knomura/museum/GPS/node11.html
おとぶさんの説が正しかったのに私が間違えてしまいました。
大変失礼しました。
おとぶさんゴメンナサイ〜〜〜m(_ _)m
しかし、難し過ぎますね。お手上げです。
情報ありがとうございます。
これで1ヶ月間くらいは、自身持って正しく答えられそうです。
半年くらいすると、また早くなるんだっけ遅くなるんだっけ、ってなりそうですが。
>Dさん
これは難しすぎます。1/2の確率で当たったというレベルです。勉強になりました。
盛り上がってますね、相対性理論。
”楽しいと時間が早く過ぎる”というのは、全く言い得て妙です。”楽しい=重力が小さい”と定義すれば、一般相対性理論が成り立ちますね。逆に、苦しいと時間が長く感じるのは、”苦しい=重力が大きい”です。これも成り立ちます。
実際に、”大きい物体は動きが遅い”というのも、質量の大きい物体が空間と光を曲げ、時間を遅らせるという事で証明できそうです。
”ゴジラの周り”では、時間は遅く流れ、空間が歪んでくれないと、絵にならない訳で。ミニチュアでは、重力が小さ過ぎるから、映像では無理があるんですね。
つまり、相対性理論とは、日常生活に普通に垣間見る事の出来る理論でもありそうですね。
>同じ速度で動いていても、小さいと速く見え、大きいと遅く見える
それってもしかしたら、大きい人(足の長い人)より小さい人(足の短い人)のほうがピッチを速くしないと同じ速度で歩けない、という意味だったりしませんか?。
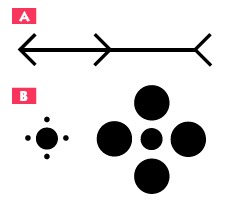
さとさん>同じ速度で動いていても、小さいと速く見え、大きいと遅く見える
それは、図のような目の錯覚の一種ではないかと思いました。
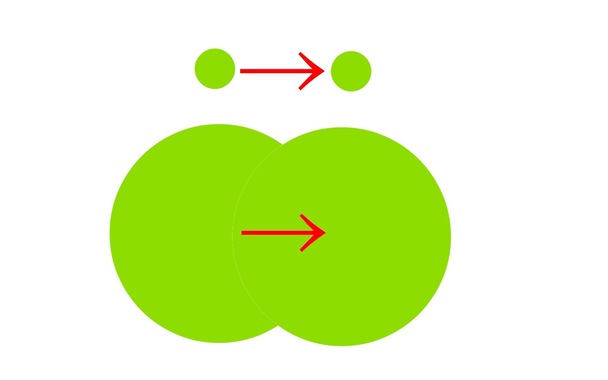
さっきの図は、人間の目は相対的に大きさを判断してしまう事例なのは、よくご存知かと思います。なので、この図のように「同じ移動速度であっても、移動物で相対的に速度を判断する」から、速さも錯覚が起きるんじゃないかな〜と。
*図は単純な図なのでアレですけど、モーションブラーとか使って表すと錯覚がより分かりやすく図示できそう。
であれば、両者をそれぞれ別々に、画面一杯に入れた動画を撮れば、身長1mの人は身長2mの人の2倍速く移動しているように見えるんじゃないかな〜と。
なので、移動物と周囲の物体との関係で大きさや移動速度は相対的に変わるんじゃないかな〜。
あと、遠くを飛ぶ飛行機と近くの飛行機では、同じ速度でも速さが違うように見えたりもしますね。
じゃあほとんど算数に関係ないこの問題といてください
くま+ねこ=?

ふふふ、楽勝だな…>それってもしかしたら、大きい人(足の長い人)より小さい人(足の短い人)のほうがピッチを速くしないと同じ速度で歩けない、という意味
>身長2mの人が1m/sで移動するのと、身長1mの人が1m/sで移動するのとでは、身長に対する進み方の割合が2倍も違いますよね。
そうです。そのつもりで書いていました。
身長30㎝のフィギュアが、腕を上から下に
「ブン!」
と振って相手を叩いたとしたら、
それと同じ速度で身長何十メートルのゴジラが腕を振る場合、
「ブォォーーーーーン!」
と時間がかかると思うんですよね。
もし30cmのフィギュアが「ブン!」と振った映像を拡大しても、全くゴジラが大きく見えず、リアリティの無いおもちゃっぽい映像に見えるんだと思います。
だからフィギュアを撮影する場合は、超スローモーションで動かさないとダメなんだーと(あの監督はわかってないな的な事を)友人が言っていた気がします。
その時は意味がわからなかったので、不明ですが。
え、相対性理論って、そんなに適当な話なんですか??(笑)
ますますよくわからなくなりました。
現実に、衛星では時計の進むスピードが違うとか聞くと、「おおー!」と思いましたが、日常生活に普通に垣間見る事の出来る理論なんでしょうか…
相対的に、遅く見えたり速く見えたり、というのはありますよね。
遠くの飛行機が遅く見えるのは、あれ何でしょうね。(全然わからん)
”ほんとに厄介なのは、相対性理論に深く根を張るリーマン幾何学だ”とコメントした様に、”リーマン幾何学が会得できたなら、一般相対性理論は呆気ない程簡単に言い表す事が出来る”と。あくまで、リーマン幾何学に比べたらですがね。しかし、そこへたどり着くまでに多くの学生がリーマンに撃墜されてしまうと。
”象が転んだ”ブログを参照にです。
>身長30㎝のフィギュアが、腕を上から下に
>「ブン!」
>と振って相手を叩いたとしたら、
>それと同じ速度で身長何十メートルのゴジラが腕を振る場合、
>「ブォォーーーーーン!」
>と時間がかかると思うんですよね。
身長2mの着ぐるみゴジラが、1秒で腕を上から下に振り下ろしたとすると、それと同じ速度で、身長20mのゴジラが腕を上から下に振り下ろすと、距離が10倍になりますので、かかる時間も10倍の10秒になります。
一方で、ガリレオ・ガリレイの実験で有名な通り、軽い腕も重い腕も落下する速度は一定ですから、力を加えずに腕を振り下ろした場合には、本当に10倍の時間がかかると考えて良いのかもしれません。
従って、本当に10倍の身長のゴジラの動きを映画で再現しようとするなら、10倍のスローモーションにしないといけないということですね。多分。
〉遠くの飛行機が遅く見えるのは、あれ何でしょうね。(全然わからん)
遠近法で考えてみると分かるのでは?
目前の物体が時速100kmで動く場合は1秒に約28m動くので、ビビって仰け反る迫力ありますよね。
でも、すっごい遠い物体が1秒に28m動いた場合、何キロも先のものなら、動いたのか動いてないのか分からない程度の移動距離です。
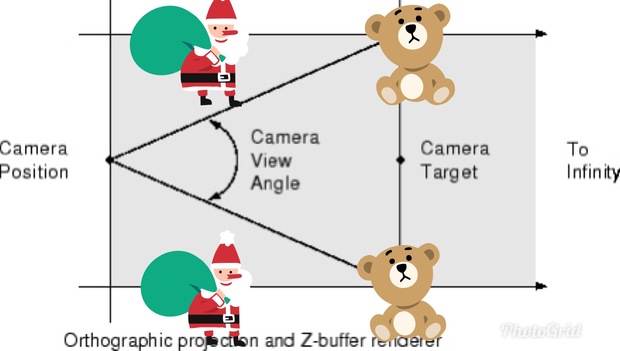
数学的に正しい説明になるか?はともかく…人間が物をみるとき、移動物は角速度的に捉えていると思います。
図の上の線から下の線まで、クマもサンタも1秒で移動する場合、速度は同じですが、クマの場合、視点からのviewangleは40度程度の移動量になります。
視点に近い目前のサンタは180度近い移動量になるので、目前の方が大きく動いているように見えるのではないかと。
当然、物体がかなり遠くなれば遠くなるほど、viewangleはどんどん小さくなるので、移動の角度は小さくなる…はず。
>間違えてますから。
「くま+ねこ=ねこくまちゃん」が「間違い」という理由を教えて下さいな。
別の答えもあるとは思うけど、ねこくまちゃんだって一つの「答え」だよね?
問題の答えは一つとは限らないよね。
「1+1」は「2」かもしれないけど、「笑顔(ニッ)」でも良いと思うんだよね。
それはみんな「正解」で良いんじゃないかとDさんは思うんだよね。
出題者が想像していなかった新しい答えが見つかると楽しいし。
勿論、本当に間違ってると思った時には「間違い」と言って良いと思うけど、「なんで間違いなの?」と聞かれた時にちゃんと答えられるようにしておかないとね。
以上マジレスでした。
それと、間違えの理由はそのまますぎるから。ちゃんとした理由があります。もうちょい頭で考えてください。
以上マジレス返しでした。
後とっちんさん正解です。
熊(くま)+猫(ねこ)=
熊猫
中国語で熊猫(パンダ)というので、正解はパンダです。ねこくまちゃんはそのまんますぎるので不正解です。いいですね?Dさん。理由もありますし、細かくも説明できます。確かにDさんのマジレスも一理ありますが、理由も説明でき、細かく理由も説明できるので、その答えがあっているとはならないのでは?
後マジレスって聞かれた時間マイネ王開いてなかったので言えませんよ。なのに理由がないと決めつけないでください。理由もあります。細かくも説明できます。なら間違いでいいですよね?Dさんの考え(マジレス)でも。
あと聞きたいんですが、間違ってるかもしれないのに何で余裕だなって言ったんですか?ちゃんと答えてくださいね。
以上マジレスのまとめ+答え+質問
でした。
「くま+ねこ=熊猫(パンダ)」のほうがそのまんまじゃないかい!!。
それをひっくり返したねこくまちゃんのほうがみさとちゃんが期待している「正解」かな〜と思ったけど、ちょっと違ったようだね。そこは残念。
昨日の「3+3」という問題もそうだけど、もともと「6」という正解があるうえで、あえて別の答えを求めているんだから、「不正解」なんて無いんじゃないかな、ということを伝えたかったわけです。
「サンタさん」という答えも素敵だけど、「8」や「ミミ」でも間違いではないよね。そうした、間違いではないけど、みさとちゃんが期待していた答えじゃない時のレスの仕方を色々と工夫してみると良いんじゃないかな、というお話でした。
例えば、「間違いです」と言うかわりに、「そういう答えもありだけど、もう少しヒネった答えを期待してま〜す。」とか言うようにしてみたらどうかなあ。
(こういうウザいことを言うから嫌われると分かってるんだけど…ゴメンネ)
_:(´ཀ`」 ∠):
なので「みんな気をつけようね!」って事でいかがでしょうか。笑
「たまに」で良かった…

>軽く老眼 さんリーマン幾何学ですかあ。難しそう、という事だけは想像しましたが、それ以上はわかりません...
>Dさん
10倍のスローモーション、ですか。想像以上に遅くなりますね。
>トッチン さん
遠い物程小さく見えますが、見ている本人は「小さい」ではなく「遠い」と感じますよね。
昔聞いた事があるのですが、遠近感は、経験値から得る感覚だそうですね。
例えば上の図は、細長い1本の線路が遠くに続いているように感じます。
ところが、目の不自由な人が大人にになってから手術で目が見えるようになった場合、補正が効かず、この写真は三角形に見えるそうです。「これは山ですか?」と言ったりするらしいです。
で、何が言いたいかと言うと、遠近感は勝手に補正して奥行を感じるんだけど、遠くの飛行機の速度感(移動距離)は補正されないんだなあ、と思っただけです。
今後は、ツッコミコメントをする時には「(笑)」を付けると、冗談である事が通じるよ、と教えておけばよいのかな。でないと相手を怒らせる事があるよ、と。
多分そういう問題ですよね?違ったらごめんなさい。

さとさん三角にみえる話だけど、そのへんの似たような話はココにもあります。
認知とはなんなのか?面白いですよね。
http://kamakura.ryoma.co.jp/~aoki/vital/TrueLook.htm
みさとさん、なかなか堂々としたコメントをしていて、女性のコミュ力の高さに恐れ入りました〜!
さとママも、娘さんのトークに頼もしさを感じたり、タジタジになったりするのかな〜(〃ω〃)
熊猫は先日、上野に行ったので、フッと思い出したんだよね。
今は上野は昆虫展が人気みたいです。数学ではなく理科の話だけど、面白そう。
>今後は、ツッコミコメントをする時には「(笑)」を付けると、
>冗談である事が通じるよ、と教えておけばよいのかな。
私の説明が悪くてうまく伝わっていないようです、申し訳ない。
本当に伝えたかったことは、例えば「3+3=?」という問題で、「サンタさん」という答えを正解にしたいのであれば、「クリスマスシーズンに必須の『3+3』はな〜んだ?」とかしないと、何でもOKになっちゃうよ〜、ということです。
この「なぞなぞとして必要な『なぞ』」があって初めて「正解、間違い」という概念が出てくるので、「なぞ」の無い問題の場合は、「色んな解があってOK、勿論3+3=6でもOK」になるということ、つまり、「自分が想定した答え」以外を全て「間違い」にするわけにはいかないんだよ〜、ということを伝えたかったんですよね。
小学3年生には難しかったかなあ…