簡単な算数の問題、みなさんが解くのにかかった時間は?
上の問題、YOUTUBEのサムネイルで出ていました。
小学生向けの算数の問題だそうです。
わたくし恥ずかしながら「ん?」と思って少し考え込んでしまいました(笑)。
賢い人なら、3秒で解けるでしょうね。
皆さんは、この問題を解くのに、どれくらいの時間かかりましたか?
ちなみに私は3分くらい考えたかなー。
答えは下の動画でどうぞ。
【発想力の一発テスト】できる小学生には一瞬で解けてしまう図形問題【ジュニア算数オリンピック】
https://www.youtube.com/watch?v=ZDo0fiKm_gQ&t=1s
221 件のコメント
コメントするには、ログインまたはメンバー登録(無料)が必要です。


>> Dark Side of the Moon さん
私は、自分の解き方をけなされて、非常に不愉快です。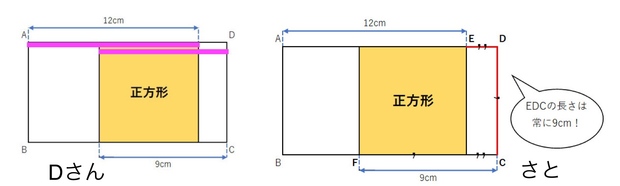
私は、Dさんの解き方を批判しているんじゃないですよ。Dさんが
「さとの解き方より、Dさんの解き方の方が優れている」
「自分以外の人は、なぜそんな複雑な計算をするのかわからない」
とディスっている事が不快なのです。
左がDさんの解き方、右が私の解き方です。
>> さと さん
そうなんですね久々にみかけたらこの図が目に入ったので・・・
スレの流れとかあんま見てないので
何があったかわかりませんが
誰の回答がというより、こんな解き方あるんだって気づいたのでコメントしました。
また面白い問題を見つけられましたら
ご紹介お待ちしてますね〜(^^)。
わたしから1問:
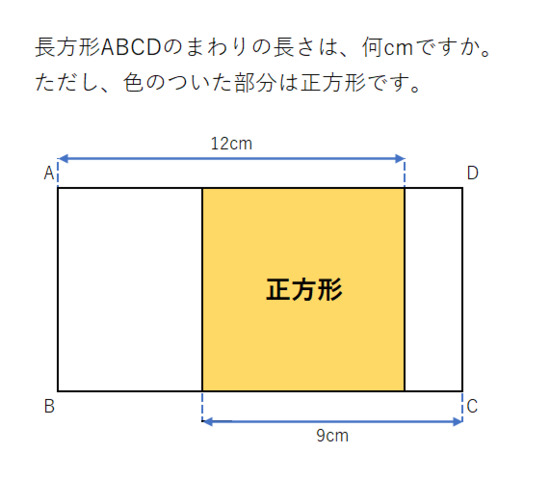
「長方形ABCDの面積が 80平方cmのとき、
正方形の1辺の長さは何cmでしょう?」
───────
いろんな解き方があるのって、
わたしは面白いと思いますよ〜〜〜(^^)。
───────
コミュニケーションポイント💞💞💞
(わたしの考えです)
「なんで〜〜」「何故〜〜」の表現は、2通りの大きく異なるメッセージの受け取り方ができてしまうので、わたしはなるべく使わないように心がけています。
①純粋に理由をお聴きしたい
②相手を責める(非難する)(ように聞こえる)
この表現形式のやっかいなところは、
言う方は①の気持ちで使うのに対して、
聞いてる方は②で受け取ることが多い、
というところでして、
意図しない誤解を招くことが多くなりがちになって使えば使うほど、せっかく仲良しになれたのに、なぜかどんどん仲が悪くなる不思議なフレーズなのです(T_T)。
理由を聞きたいときもままありますので、わたしは、「それはとても興味深いので、詳しく知りたいです。もしよろしければ、理由をお聞かせ願えませんか?」のような、肯定形+否定疑問形式の表現で、やんわりとお聞きするようにできるだけ心がけて暮らしております(^^)。
───────
>> さと さん
その2つは同じことだと思いますよ。私は、そのDさんの図とは少し違います。
下の9cmの部分は上には動かしていません。
頭の中で、上の12cmと、下の9cmを考えると、正方形の一辺がダブることになり、それは長方形の縦と同じなので、
(12+9)*2=42
です。
書き方が悪かったのかと思いますが、けなしているつもりはなく、私が見落としているなんらかの理由によって方程式や、一辺の長さを変えて検討したりしているのかなと思い、何故そのような複雑な解答をするのか分からない、教えてほしいという質問をしたつもりでした。
また、私の解き方が優れているとは全く思っていないのですが、小学生でも解けるシンプルな解答が良いのでは、とは思っています。
以上です。
>> Dark Side of the Moon さん
>ですので、分かりやすく疑問を書けば、(さとさんだけでなく)、全ての方程式を用いて回答されている皆さんに、何故そのように複雑な手順が必要なのかどうしても分からない、ということになります。気づける、気づけないというのはあると思います。すぐに気づける人はうらやましいです。
私の場合は、重なりと相殺というところから始めてしまったのですが、解き進めるうちに、要は横辺と縦辺の和がわかればいいんだから、Dさんと同じく幾何学の前提から12㎝+9㎝でいいんだと気づいた次第です。
Dさんの解き方は、(12㎝+9㎝)×2だと思いますが、さとさんの解き方も(12㎝+9㎝)×2ということになっていて、お二人ともシンプルな解き方だなぁと思いました。
単純に、わからないものを未知数で置き換えて、あとはルールを並べて機械的に解くだけで答えに到達します。頭のなかでルールの活用方法を考えないで関係を書き下すだけなので・・・
さとさんとDさんの争点は良くわかりませんが、幾何的に解くのは、以下の2種類と感じました。中点は以下のDさんの図を使います
https://king.mineo.jp/my/sato/reports/197478/comments/3834662
1. 長方形ABCDの長さを教科書通りの(AD+AB)x 2で計算する
2. 長方形ABCDの長さをABF+FC+CDE+EAで計算する
普通は1の解法に囚われます。2は柔軟な発想を必要とします(方程式は1の延長上にある)
じゃあ、1が簡単かというと、FC=9cmがHDと等しい事を使って、AE+HD-HE、そしてHEはABやCDと等しい(長方形ABCDの高さ)から、最終的に相殺されるとして解くのですが、その仮定で-HEという負の概念が出てきます。大人には解けるやり方ですが小学生にはどうだろう?と私は思います(出来る子はいます)
確か動画の解答は1に近かった気がしますが、方程式はNG(計算はOKです)、1はベター、2をベストアンサーと私はします
>> かごめそーす@🐾電脳の調律師 さん
ついで言うと、比較したのは、○△□の動画の解き方です。
こんな事考えなくても、見ただけで解けたんだなと実感しました。
>> pmaker さん
>1. 長方形ABCDの長さを教科書通りの(AD+AB)x 2で計算する2. 長方形ABCDの長さをABF+FC+CDE+EAで計算する
>確か動画の解答は1に近かった気がしますが、方程式はNG(計算はOKです)、1はベター、2をベストアンサーと私はします
さとさんもDさんも【2】で解けてると思いました。
>> pmaker さん
>単純に、わからないものを未知数で置き換えて、>あとはルールを並べて機械的に解くだけで答え
>に到達します。
なるほど、と思う部分のあるのですが、今回のように正方形の一辺をXと置き換えてみても、Xが分かるわけではなく、その後の数式でうまいことXが相殺されて消えることを期待するような解き方になるので胃が痛くなりそうです。
>> Dark Side of the Moon さん
消えないこともありますが、今回は消えるような問題なので、未知数をどう定義しても必要な条件を全て挙げていれば消えますよ解き方も大して工夫はいらないです(自然と導かれます)
今回の条件では正方形の辺の長さが確定しないまま答えが出るのは「出題者の作為」ですね
これを同じ条件でも求めるのを四角形の面積にしてしまうと確定しません
>> まいまいまいんに さん
横からありがとうございます。私はトラブル起こしやすいのですが
「なんで〜〜」「何故〜〜」の表現
私は自分が言うときも人に言われたときも
①理由を知りたい
という意味で使うし解釈するのですが
相手が②非難の意で使っていたり
批判されたと誤解してしまうことが多いのです
>理由を聞きたいときもままありますので、わたしは、「それはとても興味深いので、詳しく知りたいです。もしよろしければ、理由をお聞かせ願えませんか?」のような、肯定形+否定疑問形式の表現で、やんわりとお聞きするようにできるだけ心がけて暮らしております(^^)。
そういう言い方すればよかったのですね
ただ、家族にその言い方したら嫌味だと勘違いされそうだから言い方を考えてみます
>> pmaker さん
こんな考え方もあります。「受験算数を方程式で教えたがるお父さん」は何がいけないのか
https://wedge.ismedia.jp/articles/-/17412
…算数では具体的なことがらを対象とする場合が多く、「今わかっていることから次は何がわかるだろう? そこからさらに何がわかるだろうか?」と前から順を追って考える場面が多いです。一方、数学では一般化された定理・公式を使う場面が増え、それに当てはめて解くことが多くなるため、「わからないものをxとおく」といった方程式的な手法を使う場面が増えます。これらは問題に対するアプローチが真逆である
…しかし、両者は同じ数を扱っていても、考え方がまったく違います。数学的手法は一般化された定理への当てはめですが、算数的な図法は条件を視覚化し、感覚として捉えるものです。例えば線分図では大小関係や差、面積図では逆比の関係などを見た目にわかりやすい形で捉えることができます。
>> Dark Side of the Moon さん
Dさんが私の考えと何が違うと感じてるのか、今ひとつわかりません小学生に方程式を教えないって記事の主張に同意します
大人にとって方程式が楽ちんと言いましたが小学生向け回答では推奨しません
>> pmaker さん
数学的手法と算数的な図法の違いが分かりやすく書かれていたので、pmakerさんも同意されるのかな?、と思って紹介したものです。私の解釈では:
①数学的手法で例えば正方形の一辺をXとおくと、長方形の長辺は「12+(9-X)」で短辺は「X」となり、4辺を足すとXが消えて42となるので機械的に答えが出てきますが、何故Xが消えたのか、図形的に与えられた条件がどういう関係だったのかは分らずじまいです。
②一方で、例えば与条件の9cmの帯を12cmの帯と同じ上辺に移動させることで、「ああ、この二本の帯で長方形の長辺と短辺(正方形の一辺)の合計になってるじゃないか」と気付いて解く算数的な図法だと、図形的に与えられた条件と求める回答との関係が見た目にわかりやすい形で捉えることができます。(これはさとさんの「赤い紐、青い紐」による解き方でも同じです。)
ということで、先程のコメントで最後に引用した「算数的な図法は条件を視覚化し、感覚として捉えるものです。例えば線分図では大小関係や差、面積図では逆比の関係などを見た目にわかりやすい形で捉えることができます。」という記述に「なるほど」と大いに同意したところでした。
>> ヨッシーセブン@北京 さん
>その2つは同じこといえ、違うんです。
私は「重なり」を一切考えず(気付かず)に解きましたから。
後で詳しく図を描いて説明します。
>> さと さん
そうではなくて、9cmの一部(正方形の下辺)が、長方形の横と同じ長さであるということです。私からしたら、どちらもこの点が同じで、最終解き方は同じだと思います。
>> Dark Side of the Moon さん
なるほど!算数・数学の違いの方でしたか
私の考えでは、数字、数式は課題を抽象化したもので、それには学習・訓練が必要ですので、小学教育は現実にある理解しやすい問題に取り組んで習得すべきと思ってます
その上で、小学の算数と中学の数学では「実在しない概念」が入るか否かを境と考えてます
この実在しないものは体験してないので理解しにくいため、それを数式に抽象化するという作業は、2つの大きな事柄を同時に学習しなければならないため学習効率がガクッと下がることになります
実在しないものの例として、負の概念(先だって挙げたもの)、零の概念などがあり、整数からこれらを除いたものは「自然数」と呼ばれています
同じように未知数や抽象化の進んだ方程式・定理は、算数・数学に慣れてない小学生には理解が難しいものだと思います(理解させるのが難しいとも言えます)
一方で抽象化というものは簡略化でもあるので簡単に問題が解ける道具になります。なので記事のお父さんは、こちらの方が効率的だと思って教えようとするのでしょうね。想像力が圧倒的に足りませんけど・・
>> ヨッシーセブン@北京 さん
>最終解き方は同じだと思います。その通りで、最終的には同じです。
そこに至るまでの経緯が違います。
先日から揉めているのは、その経緯が、複雑だとかシンプルだとか言われて、けなされているんです。
今図を描く時間が無いので、簡単に文章にすると、
●ヨッシーセブンさんは、「重なり長」辺FGが、高さ(辺DC)と同じだと気付いた。
●私は、不明な「余白長」辺EDは9cmの一部(辺GC)と同じだと気付き、次に辺DCが正方形の高さ(辺EG)と同じで9cmの残り(辺FG)と気付いた。だから赤い紐の長さは常に一定。
という経緯です。
私には「重なり」という発想が皆無でした。
>> さと さん
>先日から揉めているのは、その経緯が、複雑だとか>シンプルだとか言われて、けなされているんです。
「けなされている」と思われたことについては申し訳ないと謝るしかないのですが、基本的にさとさんの「赤い紐と青い紐」の発想はシンプルで良いと思っていますし、そう書いたつもりです。👆
色々な観点がありますよね。
・考えるステップ数が少ない方が良いという考え
・小学生で習わないルールを使わないという考え
・より直観でわかる考え方(実在しない概念は使わない)が良いという考え
などなど。

ただ、よく分からなくて引っ掛かったのはこの「常に」のところでした。(私なら「EDCの長さはFCと同じ」と書きます。)これに対して上図のような説明があったので、変数とか定数とか随分難しいことを考えていることに驚き、「何故そのような検証をされたのでしょうか?」という主旨のコメントをしたのが「けなされた」という受け止め方に繋がったように思います。
けなすつもりは無かったのですが、質問の仕方が悪かったようです。申し訳ありませんでした。
>> pmaker さん
なるほど、確かに「負の概念」や「零の概念」など「実在しない概念」が入ってくると算数による図法では解決できませんね。分かりやすい説明でした。有難うございます.
>> Dark Side of the Moon さん
なぜそう考えたのかの経緯は、ざっと「3分考えてやっとわかった」と以前のコメントに書きましたが、後でもっと詳しく図示して書きます。夜になるかも。
相変わらずディスられて続けているので。
私は、ヨッシーセブンさんやDさんのように頭が良くないので、コロンブスの卵のような発想ができませんでした。なので地道に、周囲の長さを解いて行ったのです。
より小学生的な(頭が悪くて明晰ではなくステップ数が多い)考え方だと思います。詳しくは、後で書きます。
>> Dark Side of the Moon さん
後で詳しく書きますが、検証はしていませんし、計算もしていません。ヨッシーセブンさん宛コメントに書いた通りの事を、3分も考えてやっとわかった、という事です。
https://king.mineo.jp/my/sato/reports/197478/comments/3837074
>> スカイイズブルー さん
>実用的な何かに応用できるのかなァ●衣類など変形できるものを宅配便を送るとき、パッケージが細長ければ細長い程、宅配料金が上がり、立方体に近いほど、料金が下がる(笑)。宅配料金は周囲の長さで決まるので。
https://king.mineo.jp/reports/197579
●キャンプファイヤーを囲む時、より細長い形で囲む方が、大人数が参加できるので、面積を取らず効率的。
●居酒屋の鍋料理のテーブルは、同じ鍋サイズでも細長い方がたくさん座れる。
正方形だから、周囲がわかるという所が今回のポイントですもんね。
>> さと さん
いや~、面白いですね~、楽しいですね~。今はコロナだからテーブルを挟んだ対面の距離は近くない方がいいですね。>> さと さん
重なりと相殺で考えていたときは、相殺されるなんてこんなうまい話があるのか、騙されてるんじゃないかと思いました。>> Dark Side of the Moon さん
質問であってけなしていないというのは言い訳で、以下の事をずっと言い続けているではないですか。・検証や計算をするのは代数の考え方で小学生向けではない。=良くない解き方だ
・Dさんの解き方が純粋な幾何学であって最も良い解き方である。
---
私は変数も定数も計算も検証もしていません。
ですが広義で言えば、変数に当たるブラックボックスを扱っているのは、Dさんも私も他の方々も同じです。
Dさんは「重なり」をブラックボックスとして考え、私は右「余白」と「高さ」の2つをブラックボックスとして考えました。
後で図を作って説明します。
>> さと さん
>Dさんの解き方が純粋な幾何学であって最も良い解き方である。そんなことは言ってないのですが…
さとさんの「赤い紐と青い紐」の考え方も同じで良い解き方だと思うと何回も書いてますよね。
そして私が引っかかってるのは、これも何度も書いていますが、「Dさんは、EDやBFの長さが定数であると考え、私はEDもしくはBFの一方が変数であると考えた」という説明です。
実はここのところがいまだによく分かっていません。
何で私の考えに定数が出てくるのかさえも分かっていません。
それ以外にも何度か「Dさんの解き方は誰々さんの解き方と同じですね」という整理をされましたが、正直なところあれら全てが(何故同じなのか)理解できていません。
できれば、人の解き方を整理分類するのを止めて頂けるとこちらも反論しないで済みますので助かります。
>> Dark Side of the Moon さん
定数の話は前のコメントで違う、変数であると言われたので、その件は了解をしています。については、後で図で私の整理した根拠を説明します。
「重なり」を使うという考え方が、私には同じに見えたということです。
それが違うということであれば、それはわかっていなくてすみません。
>> さと さん
いや、何で定数だと言われるのかよく分からなかったので変数だと書きましたが、そもそも何で定数だと思われたのかを知りたいところです。でも、もうやめませんか、というかやめさせて頂きたいと思います。
m(_ _)m
>> Dark Side of the Moon さん
今図を作っています。そもそもは、Dさんが私の解き方は幾何学ではなく代数だ、と言ったからです。
「変数を使ったから代数だ」と言っているようでしたので、Dさんは定数なのかと想像しました。
でも定数にはなり得ないという事ですよね。
私もそう思います。
次に、「変数に値を入れて確かめた」だから代数たとおっしゃっているのかと思って、計算していませんよと説明をしようとしています。
私の中では、Dさんの考えと私の考えとの違いが明瞭であるつもりです。
ダータンスヒルビリーさんが書いていた内容です。
きっと書いても違うと言われるでしょうけどね。
>> さと さん
>そもそもは、Dさんが私の解き方は幾何学では>なく代数だ、と言ったからです。
>「変数を使ったから代数だ」と言っているようで
>したので、Dさんは定数なのかと想像しました。
もうお終いにしたかったのですが、時系列が逆なのでそこだけお伝えしておきます。
私が「幾何学」なんて言葉を使ったのは、さとさんが「定数だ」と言われたからです。その言葉を訂正しようとして初めて幾何学という言葉を使いました。👆
また、さとさんの解き方は幾何学ではなく代数だ、ということも言っていません。先程も書きましたが、解き方では無く、「変数?」を使って考えていることがよく分からないと言っただけです。
さとさんの赤い紐と青い紐による解き方については、何度も言っていますが、素敵な回答だと思います。
これでお終いにできると良いのですが…
>> Dark Side of the Moon さん
時系列で言うと、Dさん:「常に」がおかしい
→Dさんは定数で考えているのかと聞いた
Dさん:検証しているのがおかしい
Dさん:計算しているのがおかしい
という流れですよ。
・幾何学でも「常に」はおかしくない
・検証なんてしていない
・計算なんてしていない
です。
お疲れ様でした。
m(_ _)m
>> Dark Side of the Moon さん
説明する図を今作っていますよ。できたらアップします。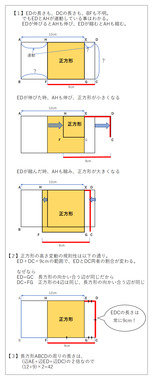
めっちゃ長い図で、すみません。端的に言うと、私の解き方は
●「余白」辺EDをブラックボックス(変数)として考えたのです。余白と高さの関係性(和が9)をなかなか見つけられず紆余曲折がありました。すぐわかった人も居られるでしょうけど。
「重なり」で解いた人は
●重なりの1辺だけをブラックボックスとして考えているので、シンプルなのです。「重なり=高さ」で終わりです。
上記を書くとDさんに嫌がられそうですが、別にDさんがこう考えていると決めつけている訳ではありません。
私の私見であって、「重なり」派と「余白」派とで、こういう差があるんだろうなと考えているという事です。
>> pmaker さん
・「重なり」を後からマイナスする方法・「余白」+「高さ」を足して行く方法
という意味ですかね?
>> かごめそーす@🐾電脳の調律師 さん
そうなんです。○△□の動画の解き方は難しいです。
>> まいまいまいんに さん
「なんで」「なぜ」の意味は、大体は文脈でわかりますよね。>> スカイイズブルー さん
スカイイズブルーさんの解き方もシンプルだと思いますよ。>> さと さん
>・「重なり」を後からマイナスする方法>・「余白」+「高さ」を足して行く方法
1. 長方形ABCDの長さを教科書通りの(AD+AB)x 2で計算する
2. 長方形ABCDの長さをABF+FC+CDE+EAで計算する
という方法ですよ
1を辺として扱う際に、さとさんの言う「重なり」という負の概念が出てくると考えてます
2はより自然に気づけるのですが、長方形の辺は(長辺+短辺)x2にこだわらない気づきが必要だろうという考えです
繰り返しますが、動画は1に近いと記憶していて、私としては1をベター、2をベストな回答としています。どちらも小学生に提示して良い回答方法と考えてます
>> Dark Side of the Moon さん
>「Dさんの解き方は誰々さんの解き方と同じですね」という整理これを図に書こうと思っていましたが、やめて欲しいという事なので、書きませんでした。
>> pmaker さん
そうですね。動画の1つめは完全な方程式。
2つめは、12cmと9cmの重複部分を引く、という解き方でしたね。
動画はかなり、数学脳(代数脳)が無いと難しそうに感じました。
私は代数が苦手です。