簡単な算数の問題、みなさんが解くのにかかった時間は?
上の問題、YOUTUBEのサムネイルで出ていました。
小学生向けの算数の問題だそうです。
わたくし恥ずかしながら「ん?」と思って少し考え込んでしまいました(笑)。
賢い人なら、3秒で解けるでしょうね。
皆さんは、この問題を解くのに、どれくらいの時間かかりましたか?
ちなみに私は3分くらい考えたかなー。
答えは下の動画でどうぞ。
【発想力の一発テスト】できる小学生には一瞬で解けてしまう図形問題【ジュニア算数オリンピック】
https://www.youtube.com/watch?v=ZDo0fiKm_gQ&t=1s
221 件のコメント
コメントするには、ログインまたはメンバー登録(無料)が必要です。


>> さと さん
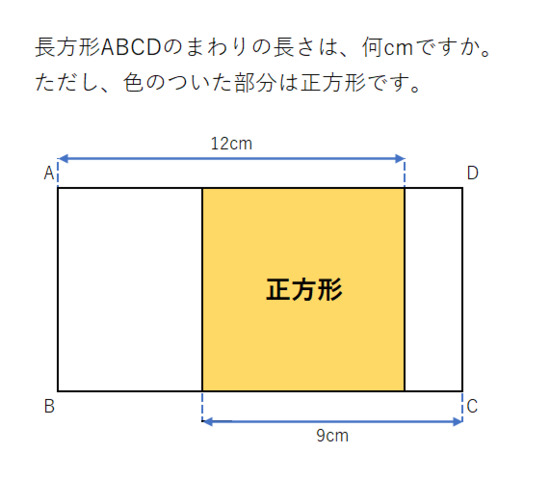
この部分だけでも十分解けそうな感じですね。>> さと さん
この部分は、正方形の一辺の長さが変わっても長方形の周りの長さは変わらないということになりますか。これは重なりと相殺の考え方で解いているときに気づきました。>> スカイイズブルー さん
そうですよ。最初からこれが出るのがベストです。
でも、紆余曲折あって、その部分がDさんに「なぜ」だと言われているので、説明をしたのです。
方程式で解いて、検証や計算をしていると言われたので、方程式は使っていませんという事を説明しているのです。
>> スカイイズブルー さん
前半の【1】の部分は、この問題を解くのに全く必要のないものです。Dさんから「常に9cm」の「常に」とは何か質問しているだけだと言われたので、回答したものです。
「これにて失礼します」と言っているので、この説明を見ていないでしょうけど。
>> スカイイズブルー さん
>正方形の一辺の長さが変わっても長方形の周りの長さは変わらないということになりますか。これは、方程式を使っていない、検証をしていない、計算をしていない、という事を説明したものです。
>> Dark Side of the Moon さん
>何で定数だと言われるのかよく分からなかったので変数だと書きましたが、そもそも何で定数だと思われたのかを知りたいところです。これは、「常に」の文言がおかしいと言われたからです。
私は逆に、なんで私が「検証している」「計算している」と思われたのかが知りたいです。検証も計算もしていません。
>> スカイイズブルー さん
もう一度書きますね。【1】の部分は、余白と高さに連動性がある事に気付いたという事です。
この時点でも「重なり」に全く気付かず、「余白」で考えていたのです。
12cmと9cmの「重なり」部分は足せない、足したらダブるという前提で考えていたという事です。
なので他の人達の「重なり」=「高さ」という発想は、あっと驚く発想の転換だと驚きました。視点が普通の周囲を足していく計算方法と異なるため。
後で考えると、結局は、余白と重なりとは、当然打ち消し合うものなので、
この問題では「重なり」を使えば、複数のステップを考える必要はなかったと気付きました。
でも、普通に単純に足していく方が、手順としてはワンステップ多いけれど、単純な考え方だとも言えると思います。
そもそも、ブラックボックスとか、X,Yとかは一切考えていません。
私の考え方では、
正方形の下辺(難しく考えればこれがブラックボックスかもしれませんが)が、正方形の右横辺と同じ長さ
だから、長方形の横の長さ
これで長方形の全ての対辺が分かるので、合計を倍にする。
です。
私は、正方形の下辺を動かして考えましたが、これでうまく行ったのはたまたまです。
多分もう少し賢いなら逆に考える方向で、
長方形の縦がわからない
これは正方形の縦と同じ
ということは正方形の下辺
の方が論理的のように思います。
>> ヨッシーセブン@北京 さん
>正方形の下辺(難しく考えればこれがブラックボックスかもしれませんが)私はそうだと思います。
>長方形の縦がわからない
>これは正方形の縦と同じ
>ということは正方形の下辺
この次に、余白+正方形の下辺 =9cm
を使って計算するという事ですよね。
「余白+正方形の下辺 =9cm」を私はなかなか気付かなかったので、ややこしい説明になりました。
が、これを数秒で気付いた人も居ると思います。
>> さと さん
正方形の一辺がブラックボックスというのは、多分感覚が異なっています。正方形の一辺の長さは全く考えていません。
正方形の一辺という概念だけです。
>> ヨッシーセブン@北京 さん
以下のいずれか、だと思いました。①重なり=高さ
だから重複した部分を引かなくていい
②余白+高さ=9cm
だから12cmに9cmを足す
---ヨッシーセブンさんは中間の以下かも?
①'重なり=高さ
だから余白+高さ=9cm
だから12cmに9cmを足す
---
私の説明がややこしいのは、②をなかなか気付かなかったという事です。きっと②を秒で気付いた人は居るでしょう。
>> ヨッシーセブン@北京 さん
>正方形の一辺の長さは全く考えていません。>正方形の一辺という概念だけです。
おおー、そういう事なんですね。
そこの感覚で、私の考えが「代数」だとか方程式だとか言われている(ような感じな)のかも。Dさんに。
私も、計算は一切していなくて、赤い紐が曲がるイメージで解いたので、代数だと言われるのは不本意なんです。
>> ヨッシーセブン@北京 さん
最初、問題が1であれば、何も考えずに、(12+9)*2になりますよね。黄色の部分が正方形であることは関係ありません。2,3も同じではないですか?
3→4の変更のときに初めて黄色が正方形であることを利用しています。
この逆の考え方で、4→1にしているということです。
理解が悪いのでわからないのですが、これはどういう意味でしょうか。
私が思うには、黄色が正方形でない場合、①の赤い帯は、9cmにならないと思います。
問題が1とは、具体的にどういうことでしょうか?
黄色い四角の底辺と余白が9cmだという条件が示されている問題ですよね?
>> ヨッシーセブン@北京 さん
>3→4の変更のときに初めて黄色が正方形であることを利用>この逆の考え方で、4→1にしている
これは、わかりますよー。
黄色い四角の底辺(重なり)を、縦棒に持って行っている、という考えですよね。
で、右余白の底辺を、右余白の上の水平な辺に持って行っているという事ですよね。
>> さと さん
そうです。言葉足らずでした。
先程の絵で、青が12cm、赤が9cmという条件で、
1の絵が示されたら、簡単にわかりますよね
ということです。
2,3もわかるのではないでしょうか?
今回、4の図が示されている問題ですが、この問題を、1に作り変えて考える
ということです。
ですので、正方形の一辺の長さは全く考えていません。
>> ヨッシーセブン@北京 さん
ヨッシーセブンさんが、図示して説明されている意図は、・重複した長さを相殺 する解き方ではなく、
・周囲(縦横)の辺を足していく計算をした
だから、計算を使わない直感的な解き方である
という事ですよね?
それはわかりますよ。
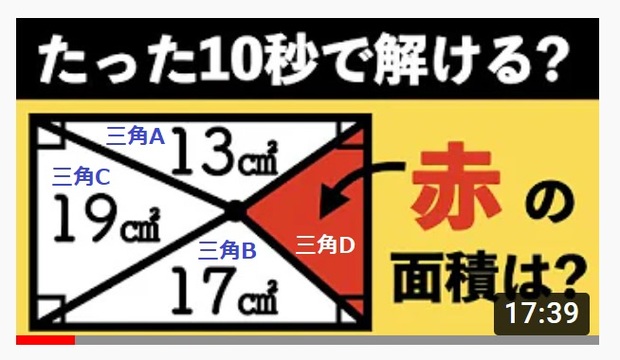
「常に9cm」と書いた「常に」について説明します。「常に」という事は、変数に値を入れて計算をして検証をしていて、幾何学的な考え方ではないと思われたと推測します。ですが検証も計算もしていません。
---
例として、上の問題の場合、
三角形Aの面積+三角形Bの面積=長方形の面積の半分
と説明する時に、
①つめの考え方:
真ん中の黒点の位置に水平線を引いて、
図示された三角形Aの高さと三角形Bの高さを足すと、長方形の高さに一致すると考える方法。
➁つめの考え方:
真ん中の黒点が、長方形の中のどの位置にあるかわからないけれども、どの位置にあったとしても、「常に」三角形Aと三角形Bの高さを足すと、長方形の高さに一致すると考える方法。
---
私の場合②つめの考え方で、真ん中の黒点が縦横無尽に移動し、三角形が刻々と変形するアニメーションが頭の中で動きます。
これは別に、変数に値を代入して確かめ算をしているのではないです。
・三角形Aの高さという不明なもの
・三角形Bの高さという不明なもの
・両者の和は常に長方形の高さ
だなと思っているだけのことです。
---
このスレの問題に戻ります。
上の例と同じで、私の頭には外側の長方形が変形するアニメーションが動きます。
それを説明したら「なぜそんな計算をするのか」と思われたようですが、計算はしていないです。
ただ紐がシャクトリ虫みたいに色んな場所で折れ曲がっているイメージをしているだけです。
・余白の幅という不明なもの
・長方形の高さという不明なもの
・両者の和は常に9cmと同じ
という事を考えているのです。
と書いてみましたが、わかって貰える気がしないですね(笑)。
アニメーションを実際に作って見せてみたら、直観的にわかって貰えるような気がするのですが…
>> さと さん
【1】EDとDCの値は変わるけれど、【2】結局ED=GC、DC=FGでEDC=9㎝となるので、
【3】で解くことができる。
という、さとさんが解答に至るまでの思考過程なのですね。これだと方程式を使った計算をしないでも答えにたどり着くことが出来る、と。
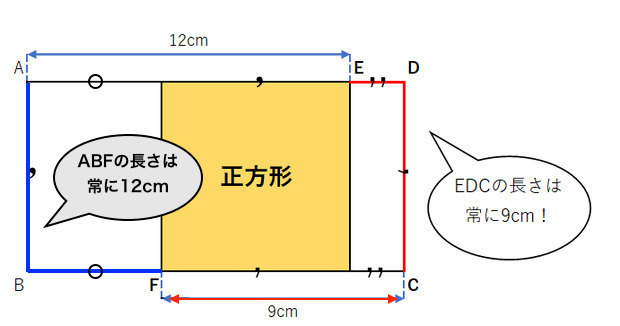
私が3分間考えた経緯を「なぜそんな事をするのか」と言われたので、書いたものです。最初にEDとDCの連動に気付き、
後から上図の「’’」「'」の辺の長さが同じ事に気付いたという経緯です。
検証もしていないし計算もしていないし代数も使っていないですよ、という事を言いたいのです。
>> ヨッシーセブン@北京 さん
>私は、正方形の下辺を動かして考えましたが、これでうまく行ったのはたまたまです。そうなんですか?
重なりが増えると、縦の太さも増える図ですよね。
>多分もう少し賢いなら逆に考える方向で、
>長方形の縦がわからない
>これは正方形の縦と同じ
>ということは正方形の下辺
>の方が論理的のように思います。
私も、その方が周囲の計算としては、理解しやすいと思います。
>> さと さん
>「常に」という事は、変数に値を入れて>計算をして検証をしていて、幾何学的な
>考え方ではないと思われたと推測します。
>ですが検証も計算もしていません。
そうでしたか、大変失礼しました。
「常に9cm」と書かれていたので、いくつかのパターンで計算しても常にEDCは9cmだった、という検証をされたのかと勘違いしてしまいました。
申し訳ありませんでした。
深くお詫び致します。
m(_ _)m
ただ、なぜ私が勘違いしたのかという理由を最後に説明させて頂くと、さとさんが「私の解き方」として説明されていた図👆から想像して、これは余白に様々な数字を入れて正方形を伸び縮みさせながら「EDCは常に9cm」であることを計算で検証されているんだなと思ってしまった次第です。
https://king.mineo.jp/my/sato/reports/197478/comments/3829058
大変失礼しました。
では、これにて失礼いたします。
>> Dark Side of the Moon さん
本当に伝わったのかな??嫌味を言われているのかな?どっちなのでしょう。そもそも、どうやって、数字を入れて検証をするのかがわからないです。
一体どんな式に数字を入れたら、「常に9cm」だとわかるのでしょうか?
私の考えた経緯は、
①余白と高さに連動性があると気付き
②次に余白=「❜❜」、高さ=「❜」と気付いた
という経緯です。それがわかるのに約3分。
最初の①に2分、②は最後の1分で気付いたと、何度も説明している通りです。
②番は私には自明の理ではなかったのです。
>> さと さん
>そもそも、どうやって、数字を入れて>検証をするのかがわからないです。
先程のさとさんの「私の解き方」の図を見て、実際に余白に0cm、2cm、6cm…などを次々と入れてEDCの長さを計算したら「常に9cmだった」という検証作業をされたのかと思った次第です。
>> Dark Side of the Moon さん
???ちょっとよくわからないので、どういう式を作ったら、検証ができるのか、という事をじっくり考えてみます。
>> Dark Side of the Moon さん
方程式を考えようと唸っていたのですが、途中で凄い事(?)に気付きました(笑)。揉めているポイントはコレだ!と思ったので、方程式を考えるのはやめました。
まず幾何学が何か、というのは、もしかしたら空間を「抽象的に」捉える事かも?と想像しました。
ヨッシーセブンさんが言っていた「正方形の一辺がブラックボックスという感覚ではなく、正方形の一辺の長さでもなく、正方形の一辺という概念だけです」という事です。これが抽象的に捉えているという事ですね、きっと。
https://king.mineo.jp/my/sato/reports/197478/comments/3839106#comment_section
例としてあげた、三角形の面積の問題ですが、
黒点に水平な横線を引いて高さを考える場合、それは高さという抽象概念で捉えていて、実際の長さという感覚ではないのでしょう。
黒点の位置は変動する、と想像した私の思考は、抽象概念ではなく、(計算はしていないけど)具体化されたイメージですね。
同じく、このスレの問題でも、「余白の幅は変動する」と考えた私の思考は、抽象的ではないですね。
ヨッシーセブンさんやDさんのように、「辺なるもの」という抽象概念が幾何学だ、という事であれば、私の「変動」思考は幾何学じゃないのでしょうね。
算数かと言えば、計算もしていないので「算数」でもなく、強いて言えば、ものさしや手のひらを広げてサイズ感を測っていく「計量」という感じですかね(笑)。実際に紐を想像して計量していた訳です。
計量がダメなのかと言えば、面倒ですけど最も原始的な方法なので、それはそれで良い面もあるのでは?とも思います(笑)。
>> さと さん
補足すると、「正方形の一辺という概念」で捉える頭脳は素晴らしいですし、シンプルでわかりやすいです。このことは、言うまでもありません。>> Dark Side of the Moon さん
もしかして嫌味を言われているのかも?という推測でコメントします。上図を証拠として
「ほら間違いなく計算していただろう。証拠はあるんだぞ。」
とDさんが詰め寄っている状態だと、そう仮定します。
私の考えた経緯は、最初に余白と高さの連動に気付いたという事です。
これが計算だという事であれば、計算と言えますね。
余白の幅+高さが一定であると気付きました。
てすから、
「高さ」=「一定の長さ」−「余白の幅」
という計算をしています。
その後で「一定の長さ」が9cmであるとわかりました。「"」「'」のルールに後で気いたのです。
ですので、まとめて「常に9cm」と書いています。
図は答えを説明するためとして後から作ったものです。
なんでそんな面倒な事を、、、という理由は、
「"」「'」のルールに最初は気付かなかったからです。
最初に気付けば、ややこしい事を考える必要は皆無でした。
>> さと さん
補足。「なぜ」というのが理由を問うているのであれば、上記の通りです。
「なぜ」というのが、意義を問うているのであれば、私が考えた経緯に無駄はあって無意味な事をしていた部分はあるでしょう。
でも批判をされるのは不当であると一貫して思っています。
それぞれの考え方に、良い面もあれば不向きな場面もあると思っています。
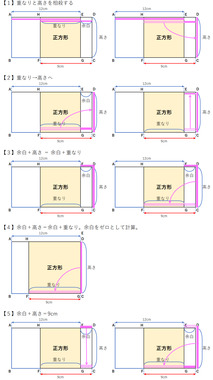
コメント欄で聞いた考え方で、5つくらいに分けられるかなあと思って図を書きました。私の解釈違いがあると思いますけど、お許し下さい(教えて貰えると嬉しいですが)
私は【3】の解き方です。
【5】は、ヨッシーセブンさんが「もう少し賢ければ(略)の方が論理的」と書いていた解き方です。
これを1発で考えた人が居られるかどうかは、コメントを読んだだけでは判断が付かないです。
>> さと さん
>私は逆に、なんで私が「検証している」>「計算している」と思われたのかが知りたいです
このコメントに対して分かりやすく答えたつもりでした。読んで頂けば、「なるほど、なぜ誤解されたのかよく分かった」あるいは「これは誤解されても多少は仕方ないかな」などと思って頂ければ有り難いかな、などと淡い期待もしてはいました。
しかし、全く期待通りにはいきませんでしたね。
「嫌味を言われているのかも?」などと、逆に火に油を注ぐ結果になったようです。
恐らくこのコメントに対してもボロクソに反論されるであろうことが目に浮かびます。
さすがに耐えられなくなってきましたので、以後このスレは非表示にさせて頂きます。
では、失礼します。
>> Dark Side of the Moon さん
いえいえ。そうでしたか。ようやく説明が伝わっていた事がわかりました。伝わって良かったです。
嫌味なのかどうか、文章では判断がつかなかったので、一応説明を繰り返したのですが、申し訳なかったです。
誤解されていたのは、わかりますよ。なので、何度も図を作って説明をしました。
伝わって良かったです。Dさんは見て下さってないだろうなと思いながら描いていましたが、見て下さっていて良かったです。
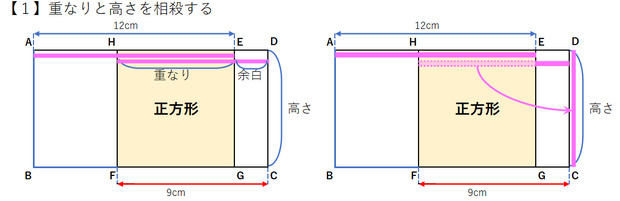
前のコメントで書いた図ですが、せっかくなので見えやすいようにバラして5つにコメントを分けて書いて行こうと思います。【1】重なりと高さを相殺 する方法
うちの中1の娘もこの解き方でした。
「重なり」に着目するという事に私は思いつかず、凄いと思いました。コロンブスの卵のような発想の転換ですね。
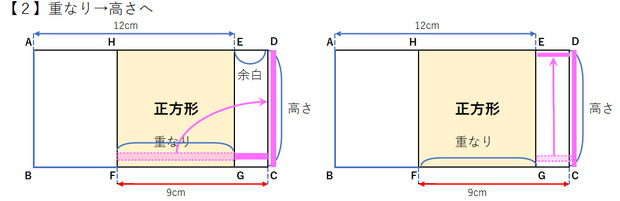
【2】重なり→高さへ持って行く方法「重なり」に着目した方法の別版。これが更に凄いですね。
重なりと高さが同じ、という事に着目して、周囲の辺の長さを足して行って計算したという方法です。
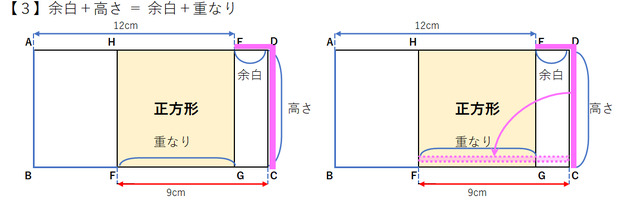
【3】余白+高さ = 余白+重なりこれは私の解き方です。
「重なり」に全く気付かず、「余白」に注目して考えました。
D点の折れ曲がり点の位置変動と、G点の位置変動が、一致するという事から考えました。
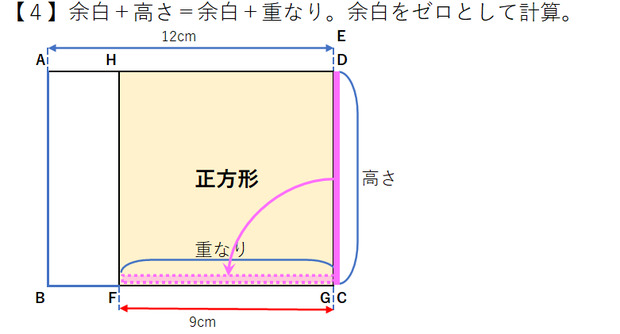
【4】余白+高さ=余白+重なり。余白をゼロとして計算。これは辺EDの余白が全く無い場合を想定して、周囲の長さを計算したものですね。
基本的には【3】と全く同じで、辺EDC=辺FC を元に考えられたものだと思います。

【5】余白+高さ=9cm私が思うには、これが最も直観的にわかりやすくシンプルな解き方に感じますね。
・周囲の辺を順番に足して行く
・長方形の向かい合う辺の長さが同じ
という直感でわかりやすいルールで解いています。
最終的には、皆さんこれに気付く訳ですけど、最初から一発でわかった人は凄いと思います。
よく式が立てられたと思います。
このスレでは、みなさん正方形の一辺を変数として計算されていましたね。
動画では、3つの変数を使って解いていました。(スゲー)
私には何を変数にするのかわからず、式を作れませんでした。
素晴らしいです。
>> Dark Side of the Moon さん
改めて読み直して申し訳なかったなと思うので、もう一度謝ります。文章から意図がわからず、嫌味の可能性があるかと思ってしまいました。
もう読んでおられないかも知れませんが、重ね重ねお詫びいたします。
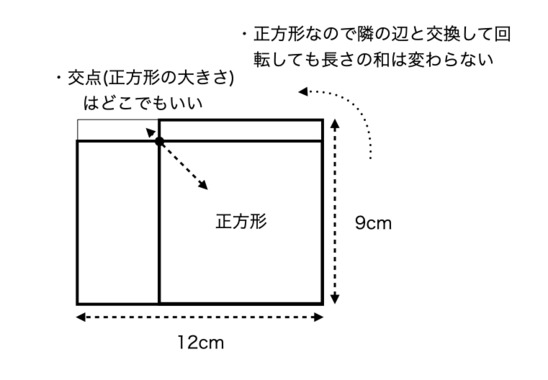
1分くらい考えて、こんなんなっちゃいました。「太線の外側はどうやっても42cmだなぁ」などと。
重なった二つの下敷きの片方をぐるっと回すみたいな。
幾何学的な解法の一例なんでしょうか(しらんけど)。
>> 流しのモバイル人@また光回線無料 さん
>重なった二つの下敷きの片方をぐるっと回すみたいな。おおー!これまた思いもよらぬ解き方です。
おもしろいですね!
でも確かにこの通りで解けますね。
L字型の周囲は、長方形の周囲と同じなのだと改めて気付きました。
このスレほんとに面白いですね。
>> 流しのモバイル人@また光回線無料 さん
正方形の左上の角の点が斜めに上がったり下がったりする感じですね。これは面白いです。
Lの文字のレタリングが、太字になったり細字になったりする感じ。
「で、なにをもとめるの?」「外の長さ?方程式かな、面倒だなぁ、サボる方法ないかなぁ」(20秒経過)
「補助線かなぁ(無駄足)」(30秒経過)
「外の長さが変わらないなら変形合体してもいいよね。あ、このベロ切り離してこっちにつけちゃえ、正方形だしピッタリでラッキー」
なんかそんな感じで、要するにめんどくさいのでなんとかならないか考えた末でした:笑。
>> 流しのモバイル人@また光回線無料 さん
>あ、このベロ切り離してこっちにつけちゃえこの発想がすごいー
正方形だから出来る技ですが、普通思い付きませんね。
我々は方程式という概念を持っているので、
解いても面白くないのかも。。。
>> ぽん太 さん
これ、方程式で解くのも難しいと思いました。わからない長さが多過ぎて、一体何を変数にするのか…
>> さと さん
正方形の一辺を変数に、、、あ、やたら簡単になっちゃった。考えて損した:笑。>> 流しのモバイル人@また光回線無料 さん
そうそう、正方形の一辺を変数にしたら簡単に解けるのですよねー。変数3つ(○△▢)を使って解く方法も動画にありました。私にはこんな解き方思い付けず解けない気がします。
https://www.youtube.com/watch?v=ZDo0fiKm_gQ&t=1s