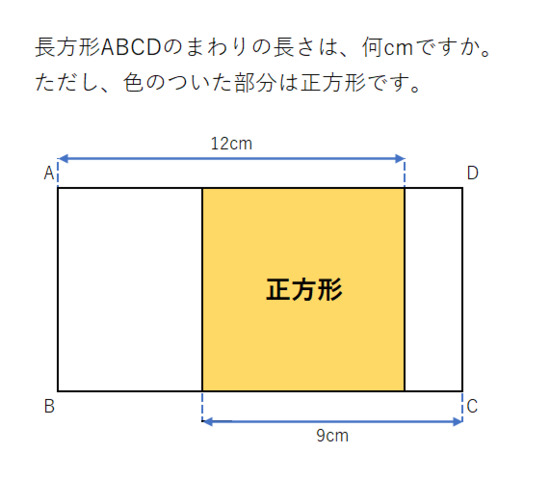
簡単な算数の問題、みなさんが解くのにかかった時間は?
上の問題、YOUTUBEのサムネイルで出ていました。
小学生向けの算数の問題だそうです。
わたくし恥ずかしながら「ん?」と思って少し考え込んでしまいました(笑)。
賢い人なら、3秒で解けるでしょうね。
皆さんは、この問題を解くのに、どれくらいの時間かかりましたか?
ちなみに私は3分くらい考えたかなー。
答えは下の動画でどうぞ。
【発想力の一発テスト】できる小学生には一瞬で解けてしまう図形問題【ジュニア算数オリンピック】
https://www.youtube.com/watch?v=ZDo0fiKm_gQ&t=1s
221 件のコメント
コメントするには、ログインまたはメンバー登録(無料)が必要です。


>> さと さん
コメントありがとうございます。もう一度見直したら理解できたというコメントを見る前に(この程度の画像でも頑張って)説明画像を作ってたのでコメント書いちゃいますね(´ω`)
最初のコメントのオレンジと黄色が色が似ていてわかりづらかったのだろうと思いつつも
あえて似た色にしたので
色を変える代わりに別の辺にも色をつけて番号も追加しました。
【回答までの経緯】
❶なにこれわからん!
でもこういう問題があるということは、数値が2ヶ所しかわかってなくても答えが出るということだ。
なんでだろ?
❷正方形と長方形がくっついてるのがヒントなのだろう。
じゃあ多分答えは両方足して2倍した42cmだろうな。ほんとかなぁ
❸(12+9)×2は(①+②+⑤+⑥)+(④+⑤+②+③)ということだ。
これでは②と⑤(オレンジ部)がダブっちゃうし、⑦と⑧(黄色部)が含まれないなぁ。
でも②⑤⑦⑧は全部同じ長さだから問題ないね。
❹青部分と赤部分がいくつでも答えが出るっておもしろ〜いᐠ( ᐛ )ᐟ
-----------------------
そして今は「実際にこの形が成り立つには正方形の一辺を何cmにしたらいいのか」が気になっています
①→a、③→b、正方形の一辺→xにしたら出るんかな?
a+x=12
b+x=9
2a+2b+4x=42
a=12-x
b=9-x
4x=42-2a-2b
2x=21-a-b
2x=21-(12-x)-(9-x)
2x=21-12+x-9+x
2x=21-21+2x
2x=2x
x=x
????
これってつまり、0より大きくて9以下なら一辺が何cmの正方形で描いてもOKという意味?
すごいねぇΣ( ºωº )
>> スカイイズブルー さん
>横に並べたことで重なっていた正方形の辺の長さが余計になるこの考え方で解いた人がかなり多いですね。
私には全く思いつかなかった解き方です。
>> 草鞋虫@わらじむしと読みます さん
ていねいな説明ありがとうございます!足してみたら重なる部分が、という解き方の人が圧倒的に多いですね。私には全く思いつかなかった解き方だったので驚きました。
私の場合❹番を最初に気付いて解いた感じです。
①④③⑥が1cm伸びたら、⑦⑧が1cm縮む、
①④③⑥が2cm伸びたら、⑦⑧が2cm縮む、
と頭の中で伸ばしたり縮めたりしたらわかって、常に周囲は一定長だという事で解きました。(正方形の1辺が0~9cmの間)
>> さと さん
> どうやって、0cmでも良いと思われましたか?図は0cmより大きいですよね。
0cmと0cm以外で、周囲の長さが同じになる理由は、どうやって考えましたか?
正方形の一辺のサイズは、必ず 0cm~9cmになります。
例えば正方形の一辺が 9cm だとすると、右側の長方形の横辺は全く空きが無いので必ず 0cm になる筈です。
もし、正方形の一辺が 8cm だったら、右側の長方形の横辺は 1cm になる筈です。
正方形の一辺が7~0cmだった場合でも、右側の長方形の横辺はそれぞれ、 2~9cmになるわけです。
ここで図形を頭の中で思い浮かべてもらうと良いのですが、正方形の一辺は、最初の図形の右の長方形の縦辺に一致するわけです。
つまりは右の長方形の横辺と縦辺の和は必ず9cmになるわけです。
文章化してみましたが、他の方の図の方が理解しやすいのかも知れませんね……。(^^;
>> Jijing さん
説明ありがとうございます。わかりました。私のこの図に近い感じですかね?
(以前のコメントと同じ図です)
右の白い長方形の幅が0に近いほど正方形が大きくなり、
幅が9に近いほど正方形が小さくなる、
という事ですよね。
だから、右の白い長方形の幅が0の時も0以外の時も、周囲の長さは同じだという理由ですね。

そうか、さとさんは正方形の大きさを変えて検証していたから「EDCの長さは常に9cm」と書かれていたのですね。「常に」の謎がやっと分かりました。私なら「EDCの長さはFCと同じ」と書きます。
>> Jijing さん
右側の白い長方形の横辺が0~9で、周囲が同じ、という考え方とすると、たぶん私と同じ考え方で導いたのでしょうね。>> Dark Side of the Moon さん
そうですね。「常に」と書いたのはEDの長さが可変(0~9cm)であるという前提で書いています。
BFの長さも可変(3~12cm)ですね。
可変なので、色んな位置で曲がる「紐」をイメージしました。
「常に」ではなく「必ず」でも良いのですけどね。
まEDの長さが問題文に指定されていないので、書かなくても、「EDの長さにかかわらず必ず」という意味にはなるのでしょうね。
>> Dark Side of the Moon さん
なんとなく解釈が違うのは、Dさんは、EDやBFの長さが定数であると考え
私は、EDもしくはBFの一方が変数であると考えた
からでしょうかねー。
EDが変われば同じようにBFも一定の規則性で変わりますので、一方だけが変数です。
EDかBFが変わればDCも変わります。
>> さと さん
>Dさんは、EDやBFの長さが定数であると考えEDやBFは変数です。定数にはなりえないと思います。
私が考えたのはシンプルで、EDはGCと同じ長さで、BFはAHと同じ長さであるという幾何学的な関係だけです。
その関係に気づけば、赤い紐と青い紐の幾何学は自ずと見えてくるはずです。
この問題は、(変数も定数も関係なく)計算を必要としない純粋幾何学の問題にしか(私には)見えません。

あ、「定数」という事じゃないのですね。私の考えた経緯が、最初にEDを変数として考えて、結果的に後から
ED=GC
DC=FG
と気付いたので「常に」と書いたのですが、
別に「常に」や「必ず」の表現が悪いとか、幾何学的じゃないわけじゃないですよね。
例えば上図の問題を説明する時、
黒点の位置が長方形の中のどこにあっても「常に」上の▽と下の△の面積の和は、長方形の面積の1/2である、と説明できますよね。
こういうのは幾何学的ではない?
幾何学の意味があんまりわからずに書いていますが。
>> さと さん
>最初にEDを変数として考えて、結果的に後から>ED=GC
>DC=FG
>と気付いたので「常に」と書いたのですが
実はこのへんが理解できていません。
図形をみれば
ED=GC
DC=FG
なのは明らかですよね。(長方形の向かい合う辺の長さは等しい)
何故そこを疑って検証されたのか、そこを疑う必要があったのか、そこの意味がよく分かっていません。
>> Dark Side of the Moon さん
解くのに3分かかったと書きましたが、すぐに解けずに色々考えてみたのです。その経緯として色んな事を頭の中でやってみたのです。
3分のうち最初の2分は気付かず、後の1分でわかった事もあるのです。
点々付けて辺の長さが同じだと書いた事は、後の1分で気付いた事です。
最初の2分は、長方形を伸ばしたり縮めたりして考えていたのです。その途中で紐を曲げる考えが出てきました。紐をもとに辺の長さが感じだと説明できるようになりました。
3秒が正しくて3分が間違いという事ではないですよね。
なんでこんなに言われないといけないのー
(T_T)
でも、このスレ見てて、この辺の長さが同じという解き方をしているひとが他に誰も居ないので、
「誰が見ても明らか」
という事はなくて、ほとんどの人は気付かない事なんじゃないですかね。私も気付くのに3分考え続けてようやく気付きましたし。
面白いですね(^^)。
それぞれの人が「あっわかった!」
というアハ体験をしているようですね!
↑この体験が楽しいですよね(^^)。
①幾何学、②代数学、③解析学
・幾何学は最古から発達した学問
・幾何学は図形の研究が目的
■数学の歴史:古代、中世、近代、現代
・古代から中世に:ユークリッド『原論』
・中世から近代に:デカルト『幾何学』
・近代から現代に:ヒルベルト『幾何学基礎』
・数学の発展のきっかけ(転換点)は幾何学
■幾何学の特徴:
・幾何学は、目に見える形から、無形の構造に至るまで、形を理解する学問。
・幾何学は、世界認識の仕方に関係します。何かを「理解した」=「イメージの形成」と言い換えられます。
・幾何学では、空間自体が抽象化され、「位相空間」または「多様体」として実体化され、具体と抽象との緊密な関係が研究されます。
・空間の対称性をまとめた集合は、それ自体ひとつの空間となる。「リー群」「微分同相群」
・種々の幾何構造理論は、対称性を線形化し、無限次元の表現空間を通じて、複素幾何、幾何的量子化、偏微分方程式、非可換幾何、大域解析、整数論、積分幾何学などの分野と関連します。
・解析学の対象でもある方程式をもつ構造では、その方程式を写像として、幾何学的に把握できます。
・多様体とその変形からなるカテゴリーを代数的に把握する「位相的量子場理論」、構造の特徴を浮き彫りにする「特性類」 など。
■非ユークリッド幾何学:
「三角形の内角の和」は180°。それはユークリッド幾何学での話。
三角形が平面じゃなくて、ボールの表面のような「球面」に描かれていたら? 内角の和は180°より大きくなります。
球面上の世界では、私たちの知っている図形の定理は当てはまらないのです。
いままでの常識が通用しない世界、「非」ユークリッド幾何学、も面白いですね(^^)
「非ユークリッド幾何学」は「ユークリッド幾何学」の公理である「直線外の1点を通り、この直線に平行に引ける直線はただひとつである」を否定し、「そういう直線が2本以上引ける」、または「ただひとつもない」という公理に置き換えた幾何学で、19世紀末に誕生しました。
発表当初は日常感覚とずれたこの幾何学の考え方は多くの批判を受けたようですね(^^)。
「図形をどう見るか」によって、いろいろな幾何学が成り立ちますね(^^)。
余談でした。
>> さと さん
>なんでこんなに言われないといけないのーありゃ、失礼しました。
私はただ下記のコメントを訂正しようとしただけだったんですが…
>Dさんは、EDやBFの長さが定数であると考え
とすぐに気が付きました。
>> ヨッシーセブン@北京 さん
Dさんが書いていたこの考え方ですね。大半の人(方程式を使わない人)がこの考え方て解いたようですね。
>> さと さん
>大半の人(方程式を使わない人)がこの考え方て解いたようですね。え、そうだったんですか?
すると、下記のコメントとの整合性は?
(と、また追求してしまう悪い癖)
>>このスレ見てて、この辺の長さが同じという
>>解き方をしているひとが他に誰も居ないので、
>> Dark Side of the Moon さん
上図の考え方と、「重なり」という考えは違うと思ったので、分けて書きました。同じという事なら、みんな同じ考えです。
私は、「重なり」を一切考えずに解いたので、別の解き方だとして分けました。

よく分らなくなってきたので、とりあえず私の見解だけを書きます。基本は「長方形の向かい合う辺の長さは等しい」という単純なことの繰り返しであり、上図で言えば、9cmのピンクの帯が「長方形の向かい合う反対側」でも同じであることに気付くことがスタートです。
次に、正方形の左右の白い長方形の向かい合う辺同士の長さも同じであることに気付けば、赤い紐と青い紐の考え方に繋がる、と言う流れなんですよね。
なので、私の整理では、「重なり」も「赤い紐と青い紐」も基本は「長方形の向かい合う辺の長さは等しい」という「幾何学的に明らかなこと」に収斂します。
以上、あくまで私の個人的見解に過ぎませんので、聞き流して下さい。
>> Dark Side of the Moon さん
私の場合、赤い紐と青い紐は、曲がる場所が変わっても常に一定の長さであると最初に考えました。正方形という条件があるからです。これは幾何学ではなく代数だという事でしょうか?
(最初にDさんが幾何学じゃないと言ってきたので)
>> Dark Side of the Moon さん
代数を使っちゃいけないだろ?ってことで、代数を使ってもどこを変数にするかによりけりで、同じにもなりますから。長方形の縦をX、横をYとするならば、
Y=12+9-X=21-Xなので、X+Y=21
周囲の長さは
2X+2Y=2(X+Y)=42
なので。
>> さと さん
算数の問題だということだったので便利な方程式を使わずに解きました。一分くらいは考えたと思います。方程式を使うとしたら正方形の一辺をxとして計算します。方程式の方だったらもっと速かったかも。考えの道筋は方程式を使っても使わなくてもそれ程差は無いように思いました。方程式を使うと使わずに解いたときには気づかなかった部分がよく見えてきて楽しい問題でした。>> まいまいまいんに さん
難しいー& 非ユークリッド面白いですね!にわかに理解できないので、ゆっくり読んで考えてみます。
>> ダータンスヒルビリー さん
>長方形の縦をX、横をYとするならば、>Y=12+9-X=21-Xなので、X+Y=21
そうですねー
上図を最初から言い当てていたのは、ダータンヒルビリーさんだけな気がします(私が読み間違いしていなければ)。
>小学生なら、12cmと9cmを足したら長方形の横の長さと正方形の一片(=長方形の縦の長さ)を足したもの
https://king.mineo.jp/my/sato/reports/197478/comments/3828497
>> スカイイズブルー さん
一分で解けたとは素晴らしいですね。「重なっている部分が余計」
「両脇の辺(縦線)と相殺」
この考えの人がほとんどですね!
うちの娘(中1)も同じ解き方をしていました。
ちなみに、私には全く思い浮かばなかった解き方です。
>正方形の一辺をxとして計算
これも私には思い浮かびませんでした💧
>> Dark Side of the Moon さん
もう一度考えてみました。昨夜から、どの解き方が最もスマートでシンプルか、という話をしていると思うのですが…
その前提で、上の解き方がスマートだ、という話でしたよね。
で私の場合は、ここに行き着くまでに紆余曲折があって、そこはまあスマートじゃないよね、というのはわかります。
で多くの人が考えている「重なる」けど「相殺される」という考えもまた、1ステップ多いのですよね。
ダータンヒルビリーさんが言ってるのが多分上図の解き方で、それが最もスマートですよね。
あと「この解き方は誰も居ない」と書いたのは私の間違いで、ダータンヒルビリーさんが書いていましたね。
>> さと さん
ダータンスヒルビリーさんの「ス」が抜けていました。失礼いたしました。>> さと さん
>「重なっている部分が余計」「両脇の辺(縦線)と相殺」
この考えの人がほとんどですね!
うちの娘(中1)も同じ解き方をしていました。
ここで行われたことは式にすると、次のようになると思います。
横の長さ=12+(9-正方形の一辺の長さ)
縦の長さ=正方形の一辺の長さ
横の長さ+縦の長さ=21
よって、周囲の長さ=(横の長さ+縦の長さ)×2=21×2=42
そうすると、ダータンスヒルビリーさんが書いていらっしゃった以下の考え方、
>長方形の縦をX、横をYとするならば、
Y=12+9-X=21-Xなので、X+Y=21
周囲の長さは
2X+2Y=2(X+Y)=42
と、そんなに変わらないようにも思いますがどうなのでしょう。
>> スカイイズブルー さん
ダータンスヒルビリーさんが書いておられる式と全く同じですね。これは、Dark Side of the Moonさんの解き方を、ダータンスヒルビリーさんが式にしたものです。
ダータンスヒルビリーさんは、小学生向けの回答は、以下が良いという考えです。
「小学生なら、12cmと9cmを足したら長方形の横の長さと正方形の一片(=長方形の縦の長さ)を足したものなので、それを2倍にしたら長方形の周りの長さになる、という解き方じゃないでしょうか?」
https://king.mineo.jp/my/sato/reports/197478/comments/3828497
>> スカイイズブルー さん
と思ったけど違ったらすみません>> さと さん
>「小学生なら、12cmと9cmを足したら長方形の横の長さと正方形の一片(=長方形の縦の長さ)を足したものなので、それを2倍にしたら長方形の周りの長さになる、という解き方じゃないでしょうか?」方程式を使わないで解くにはどうするかということですね。ただ、12cm+9cm=長方形の横の長さ+正方形の一片(=長方形の縦の長さ)には、説明にちょっと飛躍があるかもしれませんね。
>> スカイイズブルー さん
>説明にちょっと飛躍がある理由の説明じゃなくて、解き方のパターンを示しているんでしょうね。
私が読み違えている可能性もありますが。
>> スカイイズブルー さん
>方程式を使わないで解くにはどうするかということですね。そうですね。ダータンスヒルビリーズさんは、動画の解答は方程式の解き方だから、図形で解く方が小学生向けだと仰ってるんですね。
で最近2〜3日の話題は、
「さとの解き方は幾何学じゃないからタメ」
「重なりの解き方が最も純粋な幾何学」
という趣旨の事をDさんに言われて、
「不本意だー
ヾ(*`Д´*)ノ」
と私さとが泣いたり怒ったりしている訳です。
そこで
「幾何学にも色々あるんですよ」
とまいまいまいんにさんが書いてくれたり、
ダータンスヒルビリーさんが、
「幾何学の解き方も方程式の解き方も、考え方は一緒の事になり得るよ」
と書いてくれたり、そういう状態です。
で、私は「重なり」の解き方を批判する気はサラサラ無いのですが、
「私の解き方がダメなのなら、重なりの解き方だって50歩100歩だろう!」
と息巻いて怒ってる訳なんですね(笑)。
一応書いておきますが、どんな解き方にも優劣は無いですよ。好みやTPOはあるでしょうけど。
>> さと さん
何か物凄い誤解をされているようですが、>「さとの解き方は幾何学じゃないからタメ」
>「重なりの解き方が最も純粋な幾何学」
なんてことは一言も言ってないつもりです。
言いたかったのは、例えば上図で「ED=GC」なのは「長方形の向かい合う二辺の長さは等しい」という幾何学的に明らかなことなので、それを計算で導き出す必要はないのでは?
ということくらいです。
(ついでに言えば、「FG=HE=DC」なのも「正方形の各辺の長さは等しい」という幾何学的に明らかなことであり、これらから「EDC=9cm」が出て来る。)
「それを計算で導き出す必要はないのでは?」と言うのは純粋に質問のつもりでしたが、批判しているように取られたのであれば、申し訳ないです。m(_ _)m
以上でご容赦下さい。
>> Dark Side of the Moon さん
私も、正方形の高さ=長方形ABCDの高さ
という幾何学的に明らかなことを使って、計算しているのですよ。
Dさんも以下の計算をしていますよね。
>長方形の縦をX、横をYとするならば、
>Y=12+9-X=21-Xなので、X+Y=21
(ダータンスヒルビリーさんよコメントより)
計算で導き出すのがダメだというのは、どういう事ですか?
>> さと さん
>>説明にちょっと飛躍がある>理由の説明じゃなくて、解き方のパターンを示しているんでしょうね。
私が読み違えている可能性もありますが。
私が飛躍だと感じたのは、Dさんが説明された次の過程が隠れていたからではないかと思いました。
「・・・ついでに言えば、「FG=HE=DC」なのも「正方形の各辺の長さは等しい」という幾何学的に明らかなことであり、これらから「EDC=9cm」が出て来る。」(Dさんの説明より)
ここからダータンスヒルビリーさんの「12cmと9cmを足したら長方形の横の長さと正方形の一片(=長方形の縦の長さ)を足したものなので、」という説明が導かれるのではないかと思いました。
>> スカイイズブルー さん
そうですね。FG=DC
GC=ED
が隠れていると思います。
HEは関係ないですね
丁寧に書くとすればEGだと思います。
>> さと さん
>Dさんも以下の計算をしていますよね。>>長方形の縦をX、横をYとするならば、
>>Y=12+9-X=21-Xなので、X+Y=21
え、そんな計算はしていません。
計算したと言えば、
(12+9)×2
だけです。
方程式や数式で考える必要は無いと思っていますので。
方程式を使うまでもなく、(12+9)×2だけです
>> Dark Side of the Moon さん
この解き方いいですね。一番シンプルでわかりやすかも
>> Dark Side of the Moon さん
Dさんが、私が計算をしているというのは、何のことを言っているのでしょうか?(12+9)×2
だけですよ。
Dさんの解き方の場合、内部的には、正方形の一辺が重なるけれど縦の長さで相殺されるから、X-Xを省略した、という事でしょう。
ダータンヒルビリーさんが言われているのは、このことです。
>> ヨッシーセブン@北京 さん
わかりますよ。ヨッシーセブンさんの解き方に、なんの問題もありません。
今問題にしているのは、Dさんが私の解き方をけなしていることです。
>> かごめそーす@🐾電脳の調律師 さん
この解き方は、最初に私が書いた図ですよ。みんな、誤解しないでー