簡単な算数の問題、みなさんが解くのにかかった時間は?
上の問題、YOUTUBEのサムネイルで出ていました。
小学生向けの算数の問題だそうです。
わたくし恥ずかしながら「ん?」と思って少し考え込んでしまいました(笑)。
賢い人なら、3秒で解けるでしょうね。
皆さんは、この問題を解くのに、どれくらいの時間かかりましたか?
ちなみに私は3分くらい考えたかなー。
答えは下の動画でどうぞ。
【発想力の一発テスト】できる小学生には一瞬で解けてしまう図形問題【ジュニア算数オリンピック】
https://www.youtube.com/watch?v=ZDo0fiKm_gQ&t=1s
221 件のコメント
コメントするには、ログインまたはメンバー登録(無料)が必要です。


正方形の上辺と下辺が足されるので、
正方形の下辺を左辺に移動するイメージです
↔️↔️ = ↔️↕️
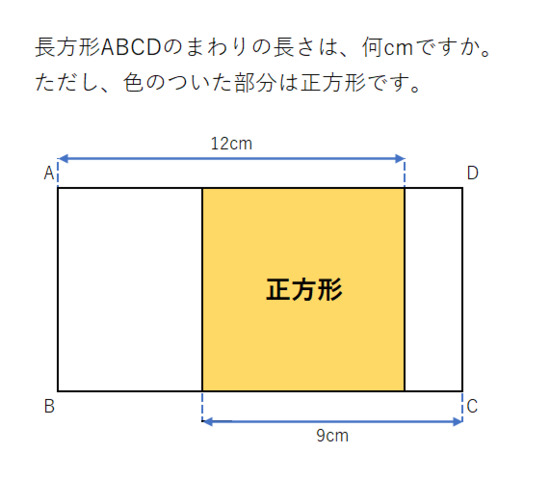
小学生なら、12cmと9cmを足したら長方形の横の長さと正方形の一片(=長方形の縦の長さ)を足したものなので、それを2倍にしたら長方形の周りの長さになる、という解き方じゃないでしょうか?
周囲 = 12 + (9-a) + 2a + (12-a) + 9
と数式にしないと分かりませんでした…
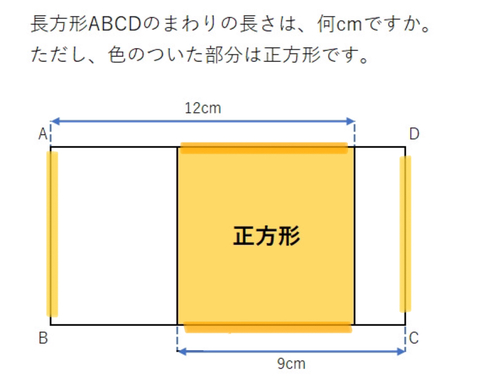
小学生向けの問題ということもあって2分考えました。わかってる数字が二つしかないんで、
とりあえずその二つを足して2倍したら答えになるんじゃないかな?
オレンジ部分がダブっちゃうけど、それって黄色部分と同じ長さだから、問題ないはず
と考えました
動画は最初の2分で飽きちゃったので答え見てない(^^;;
動画をみて納得🤔
皆さんきちんと答えてたので素晴らしいですね。
>> saru2@やらかしは不滅です🤣 さん
書いたら頭が整理できますね!>脳内記憶保持時間が年々短くなっていく
わかる~💧同じです。
>> 退会済みメンバー さん
>三分くらい考えて理解できました。おおー私と同じく3分ですね!
実生活では全く役立ちませんね(笑)
でも秒で解ける人は頭が柔らかい気がするので、脳が若返るかも知れません(しらんけど)
>> hiroaou@早寝早起き中 さん
>googleレンズは、全く同じ画像で無くても類似の画像は検索出来ます。おおーそうですか。
>前半(7分ぐらい?)の方で分かりましたが、後半の方の説明はよく分かりませんでした。
前半わかったのが凄いです。私は見る気もしなくて(笑)
>> かごめそーす@🐾電脳の調律師 さん
動画見てスッキリしたのですね!そっちの方が凄いと思います。私はよく見てもいません(笑)。丸とか四角とか三角とか何なの!と思って。
>> まいまいまいんに さん
>正方形の長さを6cm、と決めつけて、そうですね。決めつけてみると規則性がわかる、というパターンですかね。私もその方法でわかりました。
現役の頃(小学生)はめっちゃ得意だったのですが、やはり衰えてるのですね
動画はこれから見ます
>> ダータンスヒルビリー さん
>実質的には代数の解き方そうですよね。
>12cmと9cmを足したら長方形の横の長さと正方形の一片(=長方形の縦の長さ)を足したもの
そうですねー。私も9cmのヒモを90度に折り曲げる感じをイメージして解きました。
確かに。だから動画の説明がわけわからなく感じるのですね。
>> アッカリ〜ン@_@….,….,…😅 さん
おおーすごい!正方形の1辺の長さをaとして数式にしたのですね。
私には、まずそれが出来ません~
何を変数にするのかが思い付かない…
>> 草鞋虫@わらじむしと読みます さん
2分ですか。凄い!>オレンジ部分がダブっちゃう
んんん?私の頭が悪いのか図の意味が分からないです…。
動画は私も、ざっと見て諦めました(笑)
>> あまだんご さん
ちゃんと動画を見て理解した人が多くて尊敬します!説明が難しくないですか?
>> pmaker さん
方程式作って解いた人が多くてすごいです。まず、どこをどうやって方程式を作るのかが、思い付きませんでした💧
正直、前半、というか大半の時間でしたが、あれはx,yこそ使ってませんが(□とか使ってる)、未知数を使う方法で小学生の解き方ではない!ってイラってしましたが、最後にちゃんと小学生の解き方が出てきてスッキリしました
小学生向けの問題という条件では幾何的な発想で解かないとね(^^)
>> 1953生まれ さん
>小学生以下か・・・・・おもしろい(笑)
私は自分が小学生以下な事を、かなり昔から気付いていました!
しかも小学生問題なのに、2次方程式使って考えてました(笑)
でも解けない(汗)
>> pmaker さん
>最後にちゃんと小学生の解き方が出てきてスッキリ最後は小学生の解き方ですね!
でも、正方形の辺が「ゼロ」という所がなんか小学生じゃない気がしてモヤります。小学生なら自然数でしょ。
次のコメントに私の解き方を書きます。まるっきり小学生です!
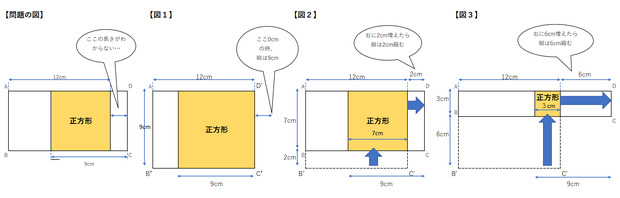
私の解き方。白い部分の幅がわからないのですが、この余白を伸び縮みさせると、長方形が横に細長くなるだけで、長方形の周りの長さは変わらないんだー、と気付いたという訳です。
>> ( ˘・з・)チェッ@君の💜にRev.🎵 さん
>2次方程式使って考えてましたおおー方程式作る時点で凄いです。
私はどうやったら方程式作れるかさえ、わかりませんでしたから。
>> ダータンスヒルビリー さん
>小学生なら、12cmと9cmを足したら長方形の横の>長さと正方形の一片(=長方形の縦の長さ)を足
>したものなので、それを2倍にしたら長方形の周り
>の長さになる、という解き方じゃないでしょうか?
ありゃ、私は小学生レベルでしたか〜〜
でも、10秒で分かりましたよ。👍
>> 草鞋虫@わらじむしと読みます さん
>オレンジ部分がダブっちゃうああー、もう一度見直したら理解できました。
なるほど。
12と9を足すと、正方形の辺の分がダブるという事ですね!こういう解き方もあるのかー面白いです。
>> Dark Side of the Moon さん
おおー10秒、もう1人ですね!すばらしいー
>> さと さん
私は問題になるから、どうせ正方形はどんな大きさであっても打ち消されると予想してましたなので、私が置いた未知数は正方形の辺でxとしました
すると正方形の左の長方形の幅が12-x、右の長方形の幅が9-xとなります
こうなるともう簡単で、全体の長方形の幅は、(12-x)+x+(9-x)、解いて21-x
全体の長方形の高さはもちろんx
で、辺を計算すると、(21-x) *2 + 2x、解いて42です
ですが、小学生向けと条件が付くと、これは正しい解き方じゃないですね・・・
私が大学生の時、小学生の塾講師をやってたことがあったのですが鶴亀算を忘れてしまって教えるのに苦労した記憶が蘇ります
代数が便利すぎて忘れちゃうんですよねぇ・・・・(^^)
>> さと さん
>私も9cmのヒモを90度に折り曲げる>感じをイメージして解きました。
私の場合はそのまんまで、12cmと9cmを足すと「ピンクの帯」になり、これは「長方形の長辺+正方形(=長方形の短辺)の一辺」と等しいことから、これを2倍すれば長方形の周長になるんじゃないか、というものでした。
解答の動画は見ていません。
まあ、間違いないかと。
理解するのに30秒ぐらいかな。3秒は直感 凄いな。(^^;
>> Dark Side of the Moon さん
三歩歩く間もなく忘れる考える蛙さんと同じ考え方ですね!https://king.mineo.jp/my/sato/reports/197478/comments/3828908
>> pmaker さん
アッカリ~ンさんと同じく、正方形の1辺の長さを変数にする計算ですね。https://king.mineo.jp/my/sato/reports/197478/comments/3828622
私は、全く思い付きませんでした。
この式を考える事が出来たら、打ち消される事に気付くでしょうけど、まず考えられない。
なぜ打ち消されると予想できたのか、そっちが不思議です。すごいです。
鶴亀算ってすごいですよね。中学受験のWebサイト見たら凄い技がいっぱいあってビックリします、全く解けません。覚えるしかないんでしょうかね。
>> Jijing さん
>右の長方形の短辺は0cmでも良いと考えたここがまず私には不思議です。
どうやって、0cmでも良いと思われましたか?
図は0cmより大きいですよね。
0cmと0cm以外で、周囲の長さが同じになる理由は、どうやって考えましたか?
>> さと さん
>わかってる数字が二つしかないんで、>とりあえずその二つを足して2倍したら
>答えになるんじゃないかな?
という手順ではなく、いきなり「ピンクの帯」のイメージができたのであまり悩みませんでした。
>> Dark Side of the Moon さん
>いきなり「ピンクの帯」のイメージができたすばらしい。なんでいきなりイメージできたのか、発想がすごいです。
>> さと さん
え〜、でも、12cmと9cmの2本の帯を並べると「ピンクの帯」そのまんまですよね。>> さと さん
>なぜ打ち消されると予想できたのか、そっちが不思議です。すごいです。所謂、「出題者の意図を読む」という奴です
正方形の値が不確定なのに出題したということは、ここの大きさが変わっても同じ答えになる、ということです。ならば最終的に消えると・・・
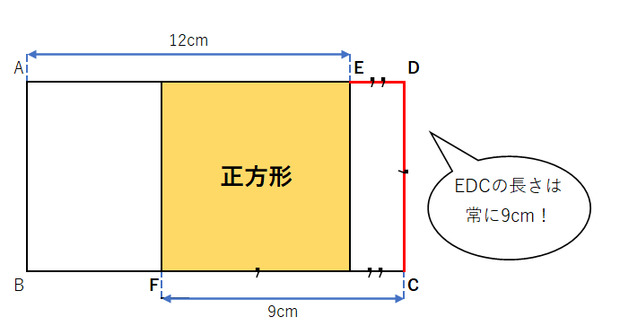
>12cmと9cmの2本の帯を並べると重ねて並べるという事自体を全く思いも付きませんでした。
私は上図のように、縦と横を順に足して行って周囲を計算するという考えでした。
重ねても、やってる計算は同じなんですけど。
重ねるという発想が無くて、重ねたら同じになるとも思い付きませんでした。
重ねるという発想は、この動画の最後の解き方の考えに近いですね。
https://youtu.be/ZDo0fiKm_gQ?t=566
>> Dark Side of the Moon さん
重なっている、という発想がこの動画の発送と近いですね。https://www.youtube.com/watch?v=ZDo0fiKm_gQ
>> pmaker さん
私が方程式にしようと思うと、正方形以外の余白の幅もわからないし、正方形の辺もわからない、と思って変数を2つ作ってしまいそうです。で、( ˘・з・)チェッ さんと同じように解けなくなってしまいますね、私も。
>> さと さん
そうそうその〇△□です途中の動画は飛ばしてみてたんですが、この部分だけ見てスッキリ~♪でした(^^
私の頭、小学生レベルってことかなw
>> かごめそーす@🐾電脳の調律師 さん
いや、あの丸 三角 四角の説明、改めて見ましたけど、ワケわからないですよ(笑)。あんな解き方絶対に絶対にできません。並べてみたら2倍になってるとか、なにそれ!?ですよー。
あれ見て理解したとかスッキリした人って、頭の中どうなっているの~
>> さと さん
>重なっている、という発想がこの動画>の発送と近いですね。
いや〜、こんなに複雑に考える意味がよく分かりません。
回答はもっとシンプルなほうが良いなあ。
>> さと さん
外周は〇+〇+〇+〇+□+□+△+△ですよね?
(〇4つの法則が成り立つのは中の四角が正方形のため)
9cmの部分は〇+△の合計長さ
12cmは〇+□の合計長さ
ということは
〇+△+〇+□=9+12=21cmになります。
外周は最初の説明のとおりなので、
21cmを2倍にした42cmが外周になる・・・すっきり~♪
>> さと さん
自分のコメントの訂正です。>正方形の辺が「ゼロ」
と書きましたが、動画ではそんな説明を全くしていませんでしたね!
重なりを横に並べてみる、という図が左です。
これは私の発想では、▢と△の幅が最大まで大きくなった状態だと思ったので、その場合高さゼロの長方形となり、真ん中の正方形の辺の長さがゼロだと思ったのです。(意味通じなかったらすみません)
>> さと さん
さとさんの「赤い紐と青い紐を折り曲げて考える」という発想もシンプルで良いように思います。>> かごめそーす@🐾電脳の調律師 さん
>私の頭、小学生レベルってことかなwいやいや、3次の複雑な代数の問題が解けて凄いと思います。
>> Dark Side of the Moon さん
この図はわかりやすいですね!>> さと さん
>3次の複雑な代数数学目線だと難解かも
○△□、個々の数字は分からなくいいのがミソですね。
レイトンのようなパズルな解き方が近いかもしれません