数字と論理で考えれば、意思疎通がもっとシンプルになる？ 「日本お笑い数学協会」横山明日希さんに、数学を学ぶ意義を聞いた

横山 明日希（よこやま あすき）
日本お笑い数学協会副会長、math channel代表。
数学の楽しさを世の中に伝えるために、「数学のお兄さん」として活動を開始。数学×お笑い、数学×恋愛など、数学と異分野を掛けあわせた独自の切り口で、数学をより身近に感じられる講演やイベントなどを開催している。著書に、『笑う数学』（KADOKAWA、「日本お笑い数学協会」名義）、『愛×数学×短歌』（河出書房新社）
TwitterID：@asunokibou

時にはインパクト重視で、数学をより面白く

そもそも「お笑い」と「数学」ってイメージがとても離れていますよね。それらを組み合わせた日本お笑い数学協会が、普段どういった活動をされているのか、全く想像ができないのですが……。

やっていることはとてもシンプルですよ。例えば「笑える数学ネタ」についてのトークイベント、数学をネタにしたお笑いイベント、小学生や社会人に向けた数学教室を開催したりしています。一見とっつきづらい数学をわかりやすく噛み砕いて、いろいろな人に面白さを知ってもらおう、というのが協会の大きな目的です。

▲ 協会会長のタカタ先生と横山さんの2名で配信している「お笑い数学ラジオ」。この回のトークテーマは「ドラゴンボール風つるかめ算」など。

例えば、小学生向けの算数教室はどのような内容ですか？　一般的な授業とはどこが違うのでしょうか。

例えば、立体図形の「円柱（えんちゅう）」と「円錐（えんすい）」がありますよね。

これは「柱（はしら）」と「錐（きり）」からそれぞれの名前がついているんですが、小学生はどっちがどっちなのか、わからなくなるようなんです。

円柱と円錐がごっちゃになってしまうんですね。

これを正しく覚えてもらうため、僕たちの授業ではピカチュウのイラストを見せるんですよ。

ピカチュウって、ポケモンの？

そうです。ピカチュウを底面にし引き伸ばして立体にしたイラストを見せて、「“ピカチュウ”柱（ちゅう）だ！」と（笑）。

ピカチュウ柱……。

子どもたちにもリピートして言ってもらいます。ピカチュウ柱がわかったら、次は錐です。カレンダーを底面にしたイラストを見てもらって、月曜日、火曜日、水曜日と……。

なんとなく、この後の展開が読めてきました。

月・火・水の3日間分のマスを錐体にしたら、「“月・火・水”錐（すい）」になりますよね。それを見せて、「さあ、みんなも言ってみよう、月・火・水錐ー！」って。こんなことをやるのが、日本お笑い数学協会の算数教室です。

覚え方がとにかく力技ですね（笑）。

インパクトが重要なんですよ。協会にはいろいろな人がいて、例えば会長のタカタ先生は、高校で数学の先生をやりながら「タカタ学園」というコンビを組んでお笑い芸人として活動しているんです。小学生からすれば、算数教室でにぎやかな大人が出てきただけで、かなり驚きますよね。

お笑い芸人さんを迎える心の準備はできていないと思います。

そこで、とっつきやすい切り口から算数についていろいろ知ってもらおうとしています。僕たちの授業を通して、少しでも「数学って楽しいな」と思ってくれるとうれしいんですが。

日常で使われる数学なら、高校レベルでほぼカバーできる

算数や数学って、世間では「勉強する必要がない」と言われることがありますよね。自分なりに理由を考えてみたところ、「高校数学は抽象度が高いから」なのかな、と思ったんです。

なるほど。

小学校で習う算数は、お釣りの額を計算したりものの数を数えたりと、生活で使う場面がとても具体的にイメージできますよね。でも、中学生・高校生の受験数学だと、そうとも言えなくなるのかな、と。

確かに、そういうこともあるかもしれません。

例えば、2次方程式のグラフのカーブがあって、「その下の面積を求めろ」と言われても、「求めたところでどうするの……？」と感じる高校生は多いのかな、と思いました。

▲ こんなやつです

その計算は、役に立たないこともないですよ。例えば、ここにペットボトルがありますよね。

はい。

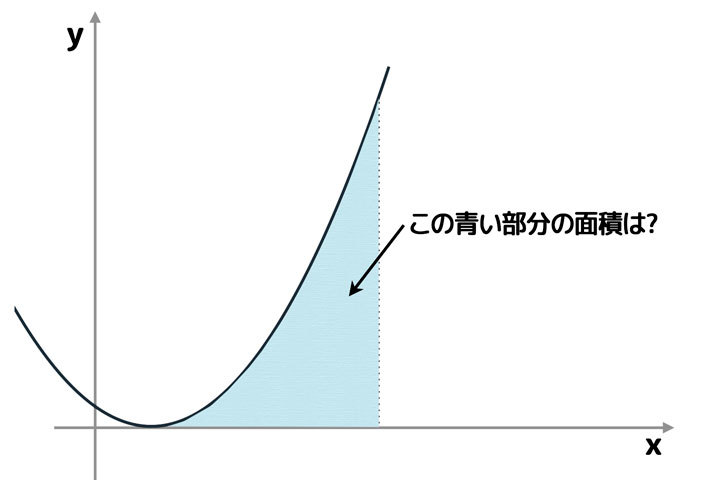
計算方法を知っていれば、ボトル表面のカーブを作図して、回転体【※1】の体積を求める公式と合わせればペットボトルの容量を求めることができます。また表面積が出せれば、ペットボトル1本を作るのに必要な素材の量もわかります。

※1 回転体：平面図形をある軸を中心に360°回転させた時に現れる立体のこと。

数学の知識が、急に実体化してきました。そんなことに応用できるとは。

ほかにも、三角関数を使えば、対象物の高さを測れるのは有名な話ですよね。伊能忠敬が日本地図を作成するのに使ったのは、その応用です。

▲ 伊能忠敬が利用した三角関数についても、授業していただきました

それほど昔から使われている知識なんですね。

積分や三角関数など、日常生活の裏で使われている数学だったら、高校生までに習った内容でほとんどカバーできますよ。「日常生活で役に立たない」と言われていますが、存在が当たり前すぎて意識されていないのかなと思います。

数学を全く意識せずとも、問題なく生活できるということですね。日常に溶け込みすぎて、勉強している最中は「今やっていることが何の役に立つのか」を知る機会は少ないのかもしれません。

論理で考えれば、深く悩みすぎることがなくなる

▲ およそ10年ぶりに「tanθ」を目にした筆者

学生時代から現在にいたるまで、勉強した数学が役に立ったり、「勉強していてよかった」と感じたりする瞬間はありますか？

役に立つことはもちろんたくさんありますよ！　大きなところでは、理屈というか、論理で物事を考えられるようになるんです。

論理的な考え方……。なんだか小難しいイメージがあるのですが。

確かに論理や理屈をとても複雑で面倒と感じる人もいますが、僕にとっては全く逆で。物事を考えるときは、感覚ではなくむしろ論理や理屈をベースにしたほうがシンプルに考えられると思います。

具体的には、どのような感じでしょうか？

例えば、寝る前に明日の予定をイメージするとします。その時、確率論から「1日で起きる出来事は、7割が想定の範囲内で、残り3割が想定外のハプニング」と僕は考えるんです。

「想定外のハプニングを想定しておく」ということでしょうか？　ちょっと矛盾するような……。

実際に経験がある人も多いと思うんですが、どんなに細かくスケジュールを計画したところで、「想定外の出来事」は絶対に起きますよね。「想定が甘かった」と考えるかもしれませんが、こういった出来事は一定以上の確率で必ず起きるんです。

そこでハプニングが起きることを前提にすれば、何が起きても、むしろ「それが正しい」と捉えられるようになりませんか？ 「ああ、3割の出来事が起きたんだな」という感じで。

その場では慌ててしまうかもしれませんが、「どうしてあんな出来事が起きたんだろう？」と必要以上に悩むことがなくなりますね。「起きたものはしょうがない。さぁ、どうしよう」と早めに切り替えられそう。

まさにそうです。論理に当てはめて考えられれば、逆に考え込んだり、深く悩んだりすることがなくなるんですよ。

数学という「共通認識」で、コミュニケーションをよりわかりやすく

数字や論理って、全てが因果関係でつながっていて、一人ひとりの価値観や感覚のような「主観」が入り込む余地がないですよね。だからこそ、自分の感情から一旦切り離すことで冷静に考えられるようになるのかもしれません。

数学の強みは、具体性と一人ひとりの主観に左右されない共通認識を持てることだと思います。「前提条件をそろえる」「言葉の定義付けをする」は、数学の基本なので。

共通認識とはどのようなものでしょう？

例えば、ある作業が「ほぼ終わった」と報告したとして、その「ほぼ」がどのくらいなのか、人によって認識は違いますよね。そこで「あとは梱包して送るだけ」と言えば、進み具合がわかるようになる。物事を伝えるときも「明日中にはできあがります」ではなく、「水曜日の午後3時まで」と言えば、コミュニケーションに齟齬が生まれにくくなります。

ぼんやりとした進捗共有が、数字を使うことでぐっと具体的になりました。主にビジネス面で役立ちそうですね。

いえ、ビジネスだけでなく、日常的なコミュニケーションでもあまり大きく変わらないと思いますよ。例えば、ランチで何を食べるか、2つのお店で迷ったとします。そんな時は、それぞれの要素を上げて、スコアを付けるんです。

「価格面は、A店は◯でB店は×」、「店までの距離は、A店は△でB店は◯」、「席数は……」みたいな感じで。条件がそろえば、「じゃあ今日はちょっと急ぐし、人数も多いから、B店だね」と決めやすくなるじゃないですか。

なるほど、算数の「条件整理」ですね。「どこに遊びに行くか？」「一日の予定をどう組むか？」といった場面でも応用できそうです。

そのほか、「服が何着あるから、一週間で何回洗濯すれば着回せるか」を考えることも数学です。論理で考えられれば、生活はもっとシンプルになるんじゃないでしょうか。

数学を使えば、女性を口説ける!?

論理を身につければ、よりシンプルに考えられるというのは、そういうことなんですね。

数学の知識や考え方は、マーケティング論や論理的思考能力みたいな、ビジネス論や、より実用的な知識として求められがちなんですよね。確かにそうした面でも使えるんですが、もっと日常的な世界と近い場所にある考え方なんだと思います。

生活に必要だし、そもそも数学はとても楽しいんだ、と。

そうです。それを実感してもらうために、興味を持つための入り口を少しでもたくさん用意しておきたいんですよね。日本お笑い数学協会の活動は、それを大きな目的にしています。ちなみに伊藤さんは、今おいくつですか？

28歳です。

すごい！　28は素晴らしい数字なんですよ。「完全数」って知ってますか？

すみません、聞き覚えはあるのですが……。

完全数は、その数自身を除く約数をすべて足した数が、元の数とイコールになる数字のことです【※2】。すごく珍しい数字で、一番小さい完全数は6、その次が28。さらにその次となると、496までないんです。

※2 完全数：28の約数は、1、2、4、7、14、28の6つ。ここから自身の数である28を除いた5つの数の総和は、1+2+4+7+14=28、となる

6歳のときに完全数と言われてもピンと来ないですし、496歳を迎えるにはだいぶ長生きしないといけませんね。

それだけ、28は素晴らしい数字なんですよ！　……これを、28歳の女性に合コンで話したらウケると思いませんか？

言われて嫌な気持ちになる人はいないと思います（笑）。

もし、相手が29歳だったら「素数だね！」となります。そのときに自分が31歳だったら、31と29は双子素数【※3】のペアなので、僕たち相性いいかもよ！ と話したら、面白がってくれる女性もいるかもしれません。

※3 双子素数：差が2である2つの素数のペアのこと。小さいものから、（3, 5）（5, 7）（11, 13）（17, 19）（29, 31）（41, 43）……とあり、無数に存在すると言われている

コミュニケーションの良いきっかけにはなりそうですが……。

「25は5の2乗」、「26は2乗すると回文数【※4】になる」、「27は立方数【※5】」などと、20代〜30代までは全ての年齢で、話題になりそうな数学ネタを用意しています。以前は「キスをしやすい身長差」を、数学を使って大真面目に計算したこともあって……。

※4 回文数：上の桁から並べても、下の桁から並べても同じ数字になる数のこと。26の2乗は676で、上から読んでも下から読んでも676になる
※5 立方数：ある数を3乗したときの解となる数字のこと。ちなみに、27は3の3乗

あの……横山さん。もしかして、数学を使って女性を口説こうとしていませんか？

あははは（笑）。でも、キャッチーでわかりやすい入り口って、結局こういうことだと思うんです。お笑いも恋愛も一緒ですよ。

義務教育で勉強する数学って、皆が同じように触れていて、知識を持っているものじゃないですか。よく考えれば、それってこれ以上にない共通認識なんですよ。なので、表面的でもいいので、数学について興味を持ってもらう機会が少しでも用意したいですね。

まとめ

論理的思考や、具体性をもった話し方とコミュニケーション、女性の口説き方に至るまで、今までは考えたこともなかった数学の新たな側面に触れることができた今回の取材。

特に論理的思考は、当たり前に身についたものと思いがちですが、もしかするとその背景には義務教育でじっくり勉強した数学の存在があるのかもしれませんね。

そして、「身の回りに必要とされる数学の知識は、ほとんどが高校で勉強する範囲で理解できる」のも驚きでした。通信やものづくり、体を動かす時にだって、その裏には数学が隠れているのかも。そんな「目に見えない数学」を意識して生活してみるのも面白そうですね！

編集：ノオト