超難問
等間隔で正方形状に並んだ9個の点。
すべての点を通るように4本の「連続する」直線を引いてみてください。
（連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です）
答えにたどり着くには柔軟で自由な発想が必要。
解けたら天才…かも
解けなかった方は下記の解答ビデオを御覧ください。
266 件のコメント
コメントするには、ログインまたはメンバー登録（無料）が必要です。
等間隔で正方形状に並んだ9個の点。
すべての点を通るように4本の「連続する」直線を引いてみてください。
（連続するというのは、1本目の直線の終点が2本目の直線の始点になるという意味です）
答えにたどり着くには柔軟で自由な発想が必要。
解けたら天才…かも
解けなかった方は下記の解答ビデオを御覧ください。
って、そういう問題じゃyないですよ（笑）
残った3人は、
ケーキは切ることなく食べらる。
最低でも何回切るのか。
ケーキなら0回、人なら1回が正解だな。
ケーキのために、
誰が自分の命を犠牲にするか、
切られるのか、
話し合いが大変だが、
おそらく、出題者が責任を持って
皆のために自決してくれることだろう。
あと、ケーキ争いから外れてもらうだけならなにもご臨終させるまでもなく、1,000円くらい渡せば済むのでは？。
△
△
△
②次は、横から水平に１回切る。（最低２回切る）
で１２個を４人で３個ずつ分ける。
これしか思い浮かばなかった、頭超固い私～
でも小３のみさとは意味を分かっていないみたい。
まだ面積を習っていないからね。
私は答え見て意味がわかった～。
結構真面目な問題だな。
分かりました！多分(笑)
答えは２回カットする、かな？(笑) ﾁｶﾞｯﾀﾗｺﾞﾒﾝﾅｻｲﾖ!
かしこーい
私が問題を出したいでーす！
？に当てはまる数を答えなさい。
む=1
あ=2
は=1
か=？
さてなんでしょう？これ分からないと私以下かもしれない…？
なんて冗談は放ったらかして。
すぐ分かられると思うから
もう一問。
次の漢字をすべて合わせニ次熟語を完成せなさい。
一 口 一 木
これもおそらく簡単です。
さあ分かるかな？
む=1
あ=2
は=1
か=？
か＝０
だね！(笑)
次の漢字をすべて合わせニ次熟語を完成せなさい。
一 口 一 木
日本！！だよね？(笑)
みんながか=0
日本
と正解を答えられたので
また違う問題♪
もっと難しい問題見つけたので書きます♪
？に入る漢字を答えなさい。
刀+8=？
多分日本と か=0を答えた人には
簡単すぎるかな？
というわけでもう一問
えーと、もはや難しさが〜…
天と地の差があります💦
問題は画像をチェック！
分かるかな？
二つとも分かった貴方は天才かも…？
やってみてね！
回復
だね！
ケーキの問題、2回カットの仕方を書けばいいのかな？
おとぶさんとマイネ神さんの答え「１回」が、ほぼ正解なんですよ～
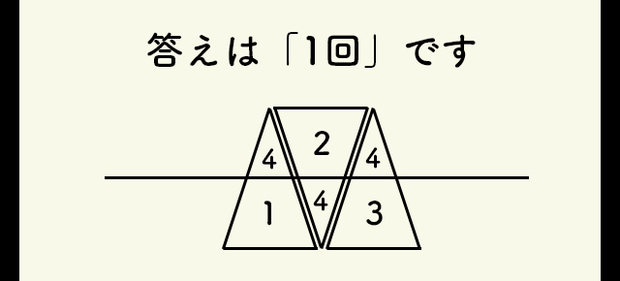
ケーキの問題、ゲームの答えの図ではこうなっていました。黒の長い線が切った所
三角がケーキで
数字の意味は…知りません（おい）
まあこれは完全に
「一回」
と言えるのでは？
真ん中のケーキを上下逆さにして3つくっつけて、一体化してからカットしたら
1回と数えられるんですか？
もうーみんな答え考え中なのに、正解書いたらダメです～
みさとちゃん
🎉正解です。🎉
👏👏👏👏👏
mvkw72さん、自力で発見されたのは凄い！
みさとちゃんも情報通だね！
たいした小学生だ。
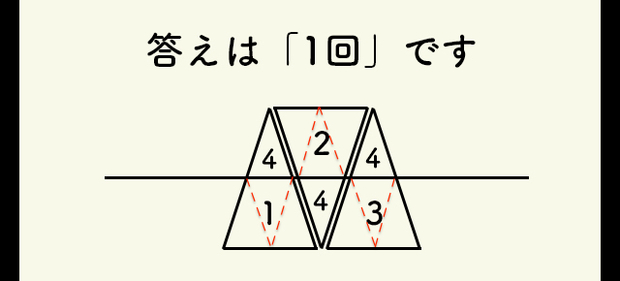
みさとちゃん>数字の意味は…知りません
切り取られた先っちょの小さい三角を三つ集めると、切り取られた残りの台形部分と同じ大きさになるんだよ。（理由はお母さんに教えてもらって下さい）
だから、図の数字は4人に分ける分け方の番号だね。
えっっ💧
だれか、小学校３年生でもわかる説明の仕方を教えて～
おとぶさーん
・三角形の面積を習っていません。
・面積という言葉を知らない
・平行を知らない
・対頂角も錯角も同位角も知らない
・内角の和も知らない
・三角4の底辺：台形１の底辺＝1:2 をどう説明するのか
紙に印刷して切り取って重ねる方法しか思いつかないよ～
チーズケーキを3つ買ってきて12ピースに切り分けるのじゃ❗
お褒めの言葉、ありがとうございます
でも、1発で分かったのではないんです
おとぶさんと同じ発想で、大きな包丁で一度に切ろう
→面積が3:1になるのは、ちょうど高さが半分のところじゃん
これ以上何を考えれば良いのか思い付きませんでした
> ほぼ正解なんだけど、その切り方だと三回になる
これを見て、分割場所は間違ってないんだろうと
後は1回と数えてもらうにはどうすれば良いかを考えました
台形の面積とか考えなくても、Darkさんの図の赤の点線で理解できると思います
赤の点線が入った図を見ても、算数の知識がないと
それっぽいで終わって、検証できないかも知れませんが
ミニいなり寿司と、普通のいなり寿司の、ご飯の量は何倍か！
って話になって、体積の話（３乗）を教えようとしたけど、
「ふーん」
で終わりました(笑)。
三角形の面積とか平行を教えてみる！
〉さとさん
折り紙を切って並べるのが、わかりやすいですよ。
算数の図形問題を教えるときは、画用紙とハサミは必須でした。画用紙を使ったのは教室の前だったからで、家では折り紙でいいのでは。
体積のときは、粘土をつかったなぁ。
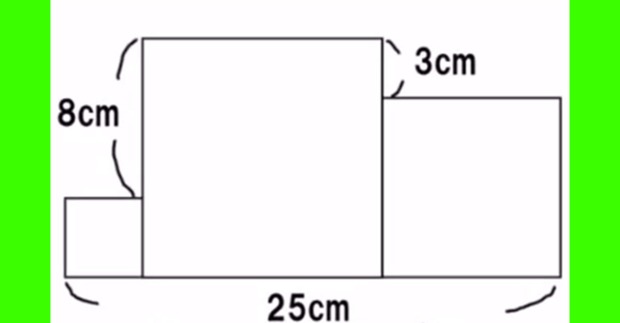
では、今度は小学4年生の問題から。上の図にある３つの正方形の合計面積を計算して下さい。
ただし、小学4年生の問題なのでXなどの変数や方程式は使えません。
ちょっと簡単過ぎかな？
では、もう一つ。こちらはいかがでしょうか？
9個で良いのかな？
大正解です❗
👏👏👏
mvkw72さん
ひっかけ問題ですいません。
左の図形なら9個で正解でした。
右上なら三角形が一つあるんですけどね（笑）
でも、もうあきちゃったかな？
右上は、コメントの削除じゃないの？
でも、その問題はDark Side of the Moon さんのコメントに書かれているから
他のユーザーには表示されないので、三角は上のコメントの違反報告か
その上のコメントは… 俺じゃん(笑)
ヒントだけ。
一番小さい正方形の上の辺を、右にド～ンとのばしてみたらわかりやすいかも。
そうか、こう見えているのは私だけでした。和差算の応用なんて使わずに、メッチャ簡単に分りますよ〜
ほぼ図形を見てのヒラメキ問題です。
3つの正方形の面積問題はできましたけど、解の導き方が正しいのかが分からない(苦笑)
別スレでケロコロさんに、もうちょっと左脳を使ったら素晴らしくなるよって言われたので、頑張って考えてみました（笑）
>もうちょっと左脳を使ったら素晴らしくなるよって
>言われたので、頑張って考えてみました（笑）
そうでしたか。
でも、今回の問題については、直感とヒラメキでお願いします。
パパパパっと、大きな正方形の3辺の合計長さが分かる「はず」です。
みさとは、折り紙で説明しなくても、Dさんの赤い点々のある図を見て、意味は理解したようです。
理由はわからないけど、三角形を半分の高さでカットしたら、面積が1対3になるらしい、という事はわかったみたい。
実は私もこの問題を機に知りました。
二等辺三角形でなくても、全ての三角形は1対3になりますね。
>実は私もこの問題を機に知りました
昨日書かれていた「体積の話（３乗）」と同じで、面積は「2乗」に比例するから、高さが半分の三角形は面積が1/4になるんですよね。
＞面積は「2乗」に比例するから、高さが半分の三角形は面積が1/4になる
高さが半分なだけでなく、底辺も半分の｢相似形｣だから、面積が1/2の1/2で1/4になるんですよね。
そもそも、高さが半分でカットしたら、底辺も半分になって相似形になるんだって事を知らなかった (というか多分習ったんでしょうけど忘れてただけですね 笑)という意味なんです。
その事を昨日わかった、という感じですねー