中学受験の問題をを中学で教わる方法で解いちゃダメでしょ
じんで@肘の君 中学受験の問題だそうです。さすが秀逸な問いですね。でもyoutubeでの解説が中学で教わる知識での回答なんだよね。
それじゃダメじゃん。まー私も最初はこの解説同様相似と比を用いた方法で解いたのですけどね。
さて問題。この問い小学生でも解けける解き方で正解を導いてください。
※本当はクイズにしたかったのですが、メッセージでは画像が添付できないから図形問題の解答は難しいよね。
ちなみにこの動画のコメントに三角形ABCを反対側にも書いて正三角形にするというのがありますが、この図からもわかるように問題文を満たす三角形は正三角形を二等分にしたものとは限らないのでその方法は不正解ですね。
49 件のコメント
コメントするには、ログインまたはメンバー登録（無料）が必要です。
二回ぐらい模試にでて解説も聞いているのですが、身についておらず。やっと理解したのは「高校物理の必殺チェック方法」の話が出てきたときでした。
※私、エレガントな解法を使わないことがあって「カレンダー問題」は毎回回答用紙の裏にカレンダーをビッシリ書いていましたｗｗ
高校受験の時、二次方程式の問題が出たんですが、
模試では一向に解けれなかったのに、
その時はすんなりと解けたので、自分が不安になり、
問題用紙、表裏一面に呪いかと思うぐらいに確認の計算式を、
書きまくった記憶があります。
(後日、答えが新聞で載っており正解してた模様。)
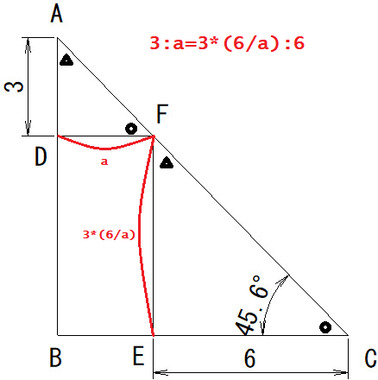
線分AC上に点Fがあれば｢18｣なのですよね?!BD = y
3x/2 + xy + 6y/2 =
(6+x)(3+y) /2 = (18 + 3x + 6y + xy) /2
3x + 2xy + 6y = 18 + 3x + 6y + xy
xy = 18
△ADF∽△FECの対応する辺の比で
3:FE=DF:6
内項の積=外項の積使って
FE×DF=18=縦×横=面積
ではいけませんか？
>> Yarthur さん
三角形ADF+四角形DBEF+三角形FEC=三角形ABCを計算しただけです。
私学の入試は、そんなものと聞いたことが…
>> ギリアム・イェーガー・ヘリオス さん
逆のパターンもあります。某有名国立高校の入試問題を中三(高1担任団がOKなら無試験で高校に進学)が見て「ウン、これなら8割イケル」。
教師「これ平均90点取らないと入試通らないから」
生徒「大問一つ落としたら不合格ジャンorz」
一方、中学の入試は0次の抽選はともかく、二次の体育・美術で2割落とされるのは理不尽だと思いましたねぇ。
３＝DF
6＝FE
縦×横＝面積
3×6＝18㎠
>> pasorin さん
えー、その問題中学受験で出るんですか。職業柄その計算を社会人になってからしたことがありますが、数列作って漸化式解いて答えだしたもんです。小学生が解けるんですか。今日考えてみます。
>> docoa@プロフ画像は変更不可 さん
数学において腕力は大切です。とにかく書きまくって法則を見つけるのはありです。>> 永芳 さん
この方法がまさに僕が最初に思い付いた解放。でもその前提は相似を使うのでそれは中学で習う範囲。比は小学校で教わるので賢い小学生なら気づくかもなんだけどね。まあ、中学受験するような子たちは進んでいますからね。
>> Yarthur さん
おーある意味シンプル。考え方は小学生でもわかりますね。でも方程式じゃ小学生わかりませんよ。>> ninnin80s さん
僕も同じように考えたのですが、相似は中学で学ぶんですよ。>> ギリアム・イェーガー・ヘリオス さん
そういう中学はだめです。中学受験ってある意味一番難しいともいわれるんですよ。小学高で習う範囲で答えを導き出さないとならないので大人は解けない。だからテレビ番組で小学生の問題が企画として成り立つんですよ。忘れたから解けないんじゃなくて大人なら別の方法で解いちゃう。
>> ギガ吉 さん
残念。角ACDは設問では与えられていません。僕は適当に作図してたまたま45.6度でしたが45度じゃないので、3＝DF
6＝FE
は満たさないんですよね。答えの18㎠はあってますけど。
何故に？？？全くそんなこと思いません。
私が採点側なら、この受験生は小学校以上のことまでよく勉強してるなあ、とむしろ感心します。
例えば小学生が方程式を使って算数の問題を解いたら不正解ですかね？？
大学受験で高校で教えない定理とか使って解答したら間違いでしょうか？？
>> じんで@肘の君 さん
相似は中学入試では必須なんですよ。教科書レベルでも相似という言葉は使いませんが、拡大と縮小という単元があります。
相似を知らずに中学入試なんで絶対できないです。
>> てんがろん さん
ここは教育の在り方を語るスレでなく小学校で習う方法でこの問題を解いてねというスレですので。ちなみに僕が採点側の場合相似の特性を利用した回答も当然正解としますが、小学校で習う範囲で解いた子とどちらか一人選びなさいという事態になったら、後者を合格させます。
それは単に知識量を競わせるのではなく、柔軟な論理力を推し量りたいからです。あくまでも私見ですが。
>> ninnin80s さん
比は習うのは認識していましたが、拡大と縮小で相似同等のことを習っているのですね。なる程。ただこの問題は、比や相似を利用しなくても解けたのでスレを立ててみました。もしもお暇があったら解いてみてください。
なお当方中学受験を乗り越えるためのテクニックには一切興味ありませんのであしからず。単純に算数の問題を解いて楽しんでいるだけです。
>> じんで@肘の君 さん
>方程式じゃ小学生わかりませんよ…いつどの計算方法を習うのか忘れてしまいました💦
また考えてみます^^;
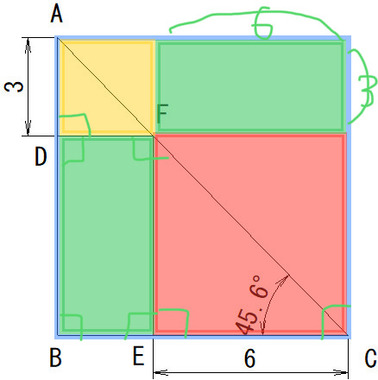
図形問題なら絵を描くです。長方形にくっついてる三角形なら直角三角形なので、
とりあえず、長方形か正方形かわかんないけど、四角くします。
可愛いくしたいので、色塗りします。
(テスト中ならかけあみで)
答えを出したい長方形と同じのもう一個できた。
可愛い♪
あれ?
3と6の長方形なんじゃない?
じゃあ面積は18 ヽ(´▽｀)/
>> 草鞋虫@わらじむしと読みます さん
と思ったけど、本当にあれが同じ長方形かわかんないw同じに見えるけど
>> 草鞋虫@わらじむしと読みます さん
でもお絵描きしたり折り紙で折ってああいう形を作ると同じ長方形二つできてた気がする
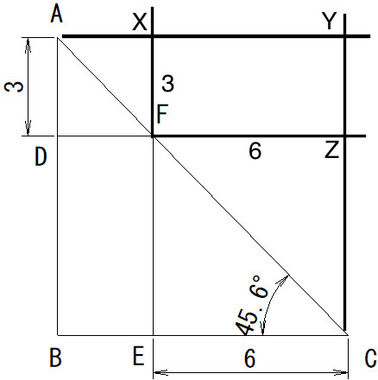
△ABC = △AYC△ADF = △AXF
△CEF = △CZF
△ABC - △ADF - △CEF = △AYC - △AXF - △CZF
□BDFE = □YXFZ = 3x6 = 18
それぞれ線分を延長した交差する点です。
式を書いていますが、絵で見てわかりますね...？
>> 草鞋虫@わらじむしと読みます さん
先を越されました(笑)正解だと思いますよ！
>> Yarthur さん
AY CY は線分を伸ばしてないですね...。BC BA と並行な直線です。
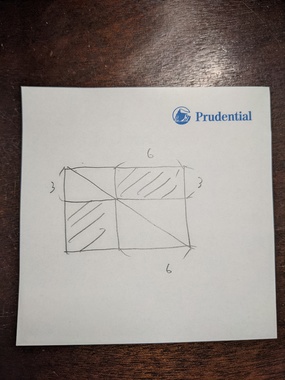
こういうことですか？細かい説明は省きますがいいですよね。
>> ninnin80s さん
そうそう、こうやって補助線引けば一発ですよね。ご名答。補助線を図のように引きます。
三角形ABCと三角形ACIは面積が等しい。
三角形ADCと三角形AFGは面積が等しい。
三角形FECと三角形FCHは面積が等しい。
三角ABCは三角形ADFと三角形FECと長方形DBEFを足したもの。
ということは、形は違うけど、長方形DBEFと長方形GFHIの面積は同じになる。
FH=EC=6 AD=GF=3 FH x GF = 6 x 3 = 18
ここに気が付くまで結構時間かかりました。
>> 草鞋虫@わらじむしと読みます さん
補助線の書き方かわいくていいですね。答えもあってます。
ただ二つの長方形は似たような形ですが、微妙に形が同じじゃないんですよ。向かい合う三角形は同じですけどね。
ということでほぼ正解止まりでした。
>> Yarthur さん
解答の書き方も完璧ですね。教科書みたい。図形問題だから補助線がミソでしたよね。中学の図形問題ってどうやって解いたらいいのかわかんないっていう子に、「とにかく補助線を書きまくる。そのうち答えが見えるよ。」って教えたもんです。ありがとうございました。
>> 草鞋虫@わらじむしと読みます さん
同じ長方形ではありませんが、面積は同じですね。>> じんで@肘の君 さん
>とにかく補助線を書きまくる...懐かしいです^^
補助線を引くと見えてくるものありましたね。
色んな角度から答えが出せる問題は面白いですね！
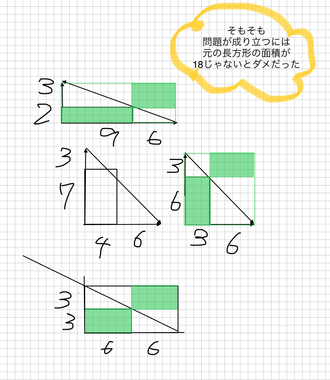
皆様ありがとうございます形は違うけど、面積同じな場合ってどんなだろう?
と思って描いてみました。
そしたら特定の条件を満たす長方形以外は、問題の図ができないことがわかりました。
できない例は図の真ん中(左)
成り立つ場合の
緑で塗られた部分は全部同じ面積
待てよ
これってもし一辺が√18(それって３√2?)の正方形をかけたら
ちゃんと図になるのかいな?
お絵描きできて楽しかったです。
ありがとうございます♪
>> ninnin80s さん
そうそう楽しいですよね。たまたま見かけた問題でしたが楽しかったのでスレあげてみました。>> Yarthur さん
>>色んな角度から答えが出せる問題は面白いですね！名言ですね。
高校の数学のテスト問題です。図形xray1oの面積を求めろ。出題者は積分で解かせたかったのですが頭のいい奴がいて、角aoxrはπ/6だからaoxrの面積ははπxr^2/6これに三角形aoy1の面積を足して回答。もちろん正解です。
>> 草鞋虫@わらじむしと読みます さん
いろいろご丁寧に作図お疲れさまでした。なんだろ。これはタブレットで書かれたのかな。ちなみに僕はPCのCADで書きました。>> じんで@肘の君 さん
パソコン使えないのでiPadですPDFの方眼紙をスクショして
そこにiPadの写真アプリについてる編集機能で
矢印(直線)や四角形を載せたり、指で数字を書いたり、
字が下手すぎるのでテキストを挿入したり
しました
>> じんで@肘の君 さん
少なくても四谷大塚で出題されました。小学生の私は……腕力で解こうと考えました。1:1層目の長さは〇ｘ3.14
2:2層目の長さは(〇+□)x3.14
3:これを(〇+何とか層目x□)が△になるまで繰り返し足し算……計算量が多すぎてムリ
※厚さ1cmのトイレットペーパーなら計算量すくないのに！
とあきらめたのですが、このトイレットペーパーを切り開いたものが「短辺〇x3.14、長辺△x3.14、高さ(△-〇)/2」の台形になると考えればわかりやすい。(メートル単位の答なので誤差の範囲で済みますが)ギザギザが気になるなら2つ反対向きに重ねて長方形にして半分で割ればいい。
結局のところ「巻いたトイレットペーパーの断面の面積＝□ｘペーパーロールの長さの面積」で、小学生でも面積の概念をきちんと理解していれば解けます(だからディメンジョンチェックの話が出た時に「アレか！」と思った)。
単位で混乱して間違った回答になる可能性はありますが、解法がわかっているので部分点はもらえるでしょう。
>> ninnin80s さん
相似は必須ですよ。でもわかりにくいんだと思う。家庭教師をするために、昔行っていた塾に行って話を聞いたついでに教えることになったのですが、「幅1mのテーブルの上1mにランプがあって、テーブルの高さが1mの場合に床にできる影の長さは？」って問題を理解できない子がいました。
※大人になると「点光源じゃないとねぇ？」とか言いそうｗ
>> じんで@肘の君 さん
扇と三角形にわけたほうがイメージつきやすいですね^^僕もそっちで計算しちゃいそう...。
1/4円から弓を引くのもありだけど、普通に足したほうが早そう^^;
>> pasorin さん
いきなり立体的な相似はハードルが高いですよ（笑）まぁ結局平面に置き換えるんですけど。
まずは電灯と人の影の長さの問題をやり込んでからですね。
>> ninnin80s さん
さすがに影の長さは？であって、影の面積は？にはなりませんよ(笑)>> 草鞋虫@わらじむしと読みます さん
マス目は方眼のpdf（そもそもそんなのあるのね）をスクショしたんだ。皆さん発想が自由でいいねぇ。てっきりお絵かきソフトのグリッド機能でも使ったのかと思いましたよ。そういえばたまーにしかスレを上げない僕ですがいつもコメントくれますよね。ありがとうございます。
>> pasorin さん
その問題については比が分からないというより、問題文の意味が分からない、つまりはこうやって絵にする読解力不足というオチではないでしょうか。読解力案外高校生でもないんですよね今は。>> pasorin さん
すごーい、流石四谷大塚！！こういうことなのね。これでまた一つ賢くなった。イェーイ。
（代数やπを使って表しちゃったけど）
>> じんで@肘の君 さん
四谷大塚がそういう解法したのではなく、私の思考経路です。小学生にシャーペンで線を引いて「面積を求めよ」と言ってもピンと来なくて「え？線でしょ？」と思うのと同様、トイレットペーパーの断面の面積って概念を想像できないんですよね。