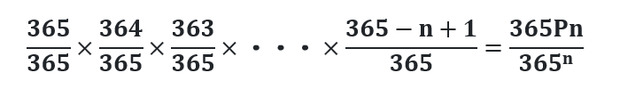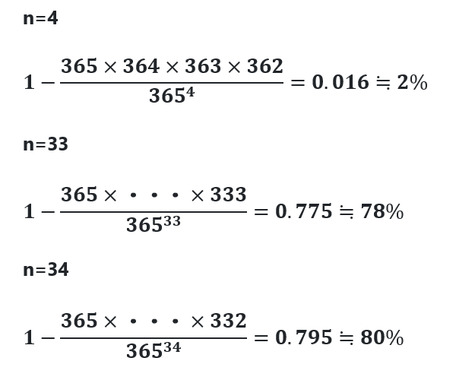公開終了
回答はあなたのターン数です
-
【問題】令和2年4月にマイネオ中学校に入学した学年の1クラスの生徒の人数を下の情報を手がかりにターン数で回答してください。
【情報】
■この学年の生徒全員の人数は同じ誕生日の生徒がいる確率が理論上80%であった。
■この学年の生徒には双子はいなかった。
■この学年は2クラスであった。
正解者で500Mb山分けです。正解順に報酬の割合は増えます。
正解者が1人の場合は500Mb独り占めですネ。
質問がありましたらコメントでよろしくお願いします。
| 難易度 | パケット獲得 | 1回 | |
|---|---|---|---|
| フロア | 1階 | 挑戦者数 | 58人 |
| クリア人数(率) | 31人(53.4%) |
|---|---|
| 平均クリア時間 | 00:01:44 |
| 公開日時 | 2020年11月01日(日) 17:00 |
|---|---|
| ランキング終了日時 | 2020年11月04日(水) 17:00 |
| 公開終了日時 | 2023年05月14日(日) 20:00 |
クリア時の獲得パケット
| 初期設定 | -- |
|---|---|
| 残りのパケット |
|
ランキング上位者の獲得パケット
1位 |
2位 |
3位 |
|---|---|---|
| -- | -- | -- |
ダンジョンを探索する
※ ご利用環境によっては、ゲームプレイ(Loading)に時間を要する可能性がございます。
ランキング
ランキング終了日が過ぎているため更新されません。
2020/11/04 時点
| 順位 | メンバー | ターン数 | パケット数 |
|---|---|---|---|
|
1位 |
3ターン
(2020/11/01 18:58) |
- | |
|
2位 |
yoshi君さん |
4ターン
(2020/11/01 18:32) |
- |
|
3位 |
|
4ターン
(2020/11/02 08:50) |
- |
| 4位 |
はっちゃくさん |
5ターン
(2020/11/01 17:26) |
- |
| 5位 |
6ターン
(2020/11/01 17:18) |
- | |
| 6位 |
ちゃちゃきさん |
8ターン
(2020/11/01 17:11) |
- |
| 7位 |
|
10ターン
(2020/11/01 18:54) |
- |
| 8位 |
15ターン
(2020/11/02 07:41) |
- | |
| 9位 |
16ターン
(2020/11/01 22:13) |
- | |
| 10位 |
銅座さん |
17ターン
(2020/11/01 18:26) |
- |
| 11位 |
太陽娘さん |
17ターン
(2020/11/01 20:24) |
- |
| 12位 |
まりりっちさん |
17ターン
(2020/11/01 22:55) |
- |
| 13位 |
17ターン
(2020/11/02 08:22) |
- | |
| 14位 |
マークn@㊙️さん |
19ターン
(2020/11/02 07:04) |
- |
| 15位 |
mgmg5さん |
20ターン
(2020/11/01 19:31) |
- |
| 16位 |
菟さん |
20ターン
(2020/11/02 07:20) |
- |
| 17位 |
えりゅしおんさん |
20ターン
(2020/11/02 07:56) |
- |
| 18位 |
25ターン
(2020/11/02 05:50) |
- | |
| 19位 |
27ターン
(2020/11/02 16:27) |
- | |
| 20位 |
|
29ターン
(2020/11/01 20:07) |
- |
| 21位 |
たむ413さん |
35ターン
(2020/11/02 01:23) |
- |
| 22位 |
呑気呆亭さん |
35ターン
(2020/11/02 08:22) |
- |
| 23位 |
eaeh@姫爺さん |
36ターン
(2020/11/01 18:17) |
- |
| 24位 |
ゲリオン@🌷さん |
37ターン
(2020/11/01 17:06) |
- |
| 25位 |
はるかかなたさん |
38ターン
(2020/11/01 17:44) |
- |
| 26位 |
lickyさん |
40ターン
(2020/11/01 18:26) |
- |
| 27位 |
ケロロロさん |
41ターン
(2020/11/01 23:27) |
- |
| 28位 |
うーりょんさん |
164ターン
(2020/11/02 10:33) |
- |
これ以上ありません。
38件のコメント
1 - 38 / 38
2クラスあって、1クラスの人数が3人てことはあり得ないですよね。
でも、ワープしたら👑へ到着したので😅
👑を手に取るか悩みましたが手にしていました。
でも、ワープしたら👑へ到着したので😅
👑を手に取るか悩みましたが手にしていました。
スミマセン...。
まだ計算してないんです。
このくらいの数ならターン数に入るかなと問題を作りました。
今日中に計算しますので、不具合がありましたらお詫びを差し上げます...。
まだ計算してないんです。
このくらいの数ならターン数に入るかなと問題を作りました。
今日中に計算しますので、不具合がありましたらお詫びを差し上げます...。
えりんぎまいたけさん
僕がテキトーに作ったので現実では〜という考え方では当たらないかもしれませんね...。
奇跡的に当たっている可能性もありますがね...。
僕がテキトーに作ったので現実では〜という考え方では当たらないかもしれませんね...。
奇跡的に当たっている可能性もありますがね...。
思ったより参加者が少ないです...。
ひとり勝ちなんてこともあるかもしれないので、皆さんぜひ参加してみてくださいね。
コメントくださった方にはチップ1枚ではありますが参加賞のお配りもしていますので...。
ひとり勝ちなんてこともあるかもしれないので、皆さんぜひ参加してみてくださいね。
コメントくださった方にはチップ1枚ではありますが参加賞のお配りもしていますので...。
■この学年の生徒全員の人数は同じ誕生日の生徒がいる確率が理論上80%であった。
◇
同じ誕生日の生徒がいる確率しか書いてない。
すなわち、10の10倍で計算するように仕向けられた引っ掛け。
10の10倍で計算するなら、
【全生徒の人数は同じ誕生日の生徒がいるのと「同じ確率で」理論上80%であった。】
と書かれていなければならない。
または、この学年の生徒全員の人数「と」同じ誕生日の生徒がいる確率「は」理論上80%であった。
と、書かれていなければならない。
良く読むと文法がおかしい。
こう言う場合、100%引っ掛け。
(昔、ロザンの宇治原が似た問題を何処かの番組でやってた。)
◎この時点で答えは、もう出ている。
■この学年の生徒には双子はいなかった。
◇
双子でも5つ子でも、2クラスに振り分けようが、分けまいが、全生徒の人数には変化なし。
■この学年は2クラスであった。
◇
2つに分けると言う情報は要る。
答えをターン数で答えるなら、
人数はもう決まっている。
50位までしか表示されないので、
全生徒は50人。
1クラス25人が正解。
悪魔の数学ですかね?。
数学でありながら、読解力が必要で、最後は算数で答えを出す。
どうでしょうか?
◇
同じ誕生日の生徒がいる確率しか書いてない。
すなわち、10の10倍で計算するように仕向けられた引っ掛け。
10の10倍で計算するなら、
【全生徒の人数は同じ誕生日の生徒がいるのと「同じ確率で」理論上80%であった。】
と書かれていなければならない。
または、この学年の生徒全員の人数「と」同じ誕生日の生徒がいる確率「は」理論上80%であった。
と、書かれていなければならない。
良く読むと文法がおかしい。
こう言う場合、100%引っ掛け。
(昔、ロザンの宇治原が似た問題を何処かの番組でやってた。)
◎この時点で答えは、もう出ている。
■この学年の生徒には双子はいなかった。
◇
双子でも5つ子でも、2クラスに振り分けようが、分けまいが、全生徒の人数には変化なし。
■この学年は2クラスであった。
◇
2つに分けると言う情報は要る。
答えをターン数で答えるなら、
人数はもう決まっている。
50位までしか表示されないので、
全生徒は50人。
1クラス25人が正解。
悪魔の数学ですかね?。
数学でありながら、読解力が必要で、最後は算数で答えを出す。
どうでしょうか?
本気で考えるべきなのか?
ここはボケるところなのか?
え〜い
ワープして
全部屋回ってやったぜっ(笑)
う〜ん
奇数ではなさそう…個人的な意見です
こちらからは以上です
ここはボケるところなのか?
え〜い
ワープして
全部屋回ってやったぜっ(笑)
う〜ん
奇数ではなさそう…個人的な意見です
こちらからは以上です
いつもダンジョンの隅々まで回るから、一クラスの平均40人程度じゃ収まらんと思ってプレイしたら、あ~! この程度だったのですねw
少子高齢化だったらこの程度なのかな?
少子高齢化だったらこの程度なのかな?
貝殻タカヤさん
まさか文法を指摘されるとは...。
算数より日本語の文法からやり直せってことですね...。
これから問題を解く方は文法は気にせず読みとったまま回答してください...。
ひっかけ問題を作ったつもりはありませんので...。
すみませんでした。
まさか文法を指摘されるとは...。
算数より日本語の文法からやり直せってことですね...。
これから問題を解く方は文法は気にせず読みとったまま回答してください...。
ひっかけ問題を作ったつもりはありませんので...。
すみませんでした。
えりゅしおんさん
↑のコメントでも書きましたが、問題を公開してから僕自身もこの問題を解いたので、現実とは離れた解答になっているかもしれませんね。現実的な解答の可能性もありますが...。
↑のコメントでも書きましたが、問題を公開してから僕自身もこの問題を解いたので、現実とは離れた解答になっているかもしれませんね。現実的な解答の可能性もありますが...。
誕生日の条件から求まるのは学年全体の人数です。
しかし、2クラスの人数比が与えられていないので、
ひとクラス人数に対する回答は出せないはずです。
2クラスの人数は、ほぼ同数と云う主旨でしょうか??
しかし、2クラスの人数比が与えられていないので、
ひとクラス人数に対する回答は出せないはずです。
2クラスの人数は、ほぼ同数と云う主旨でしょうか??
ランキングが終了しましたので正解発表といきましょう。
1クラスの生徒の人数は・・・17人です。
銅座さん、太陽娘さん、まりりっちさん、きゃすたさん、hideri-nuさん
おめでとうございます!
1クラスの生徒の人数は・・・17人です。
銅座さん、太陽娘さん、まりりっちさん、きゃすたさん、hideri-nuさん
おめでとうございます!
500Mb山分けとなりますので、
銅座さん - 120Mb
太陽娘さん - 110Mb
まりりっちさん - 100Mb
きゃすたさん - 90Mb
hideri-nuさん - 80Mb
贈らせていただきます!
銅座さん - 120Mb
太陽娘さん - 110Mb
まりりっちさん - 100Mb
きゃすたさん - 90Mb
hideri-nuさん - 80Mb
贈らせていただきます!
同じ誕生日の生徒がいる確率は、まず誰も誕生日が一致しない確率を求めて、起こりうるすべての確率である1から引くと求まります。
令和2年4月に入学した学年は年度が365日です。
まず2人の場合を考えましょう。
1人目の誕生日は365日どれでも大丈夫です。
2人目の誕生日は1人目と一致しないため364日のうちいずれかになります。
つまり、1人目と2人目の誕生日が一致しない確率は
364/365
となるわけです。
以降、3人目、4人目・・・n人目も同様に計算します。
したがって、
令和2年4月に入学した学年は年度が365日です。
まず2人の場合を考えましょう。
1人目の誕生日は365日どれでも大丈夫です。
2人目の誕生日は1人目と一致しないため364日のうちいずれかになります。
つまり、1人目と2人目の誕生日が一致しない確率は
364/365
となるわけです。
以降、3人目、4人目・・・n人目も同様に計算します。
したがって、
34人の生徒が入学した場合、同じ誕生日の生徒がいる確率が理論上80%となります。
この学年は2クラスですので、1クラスの生徒の人数は17人となります。
この学年は2クラスですので、1クラスの生徒の人数は17人となります。
退会済みメンバーさん
ビギナー
Yarthurさん
チップありがとうございました。
解説拝見しましたが、前提に誤りが…
令和2年4月の中学入学者は、平成19年4月2日から平成20年4月1日の間に生まれ人です。
平成20年(2008年)はうるう年ですので、366日として計算する必要があります。
とはいうものの、答えはやはり17人になるかと思います。
チップありがとうございました。
解説拝見しましたが、前提に誤りが…
令和2年4月の中学入学者は、平成19年4月2日から平成20年4月1日の間に生まれ人です。
平成20年(2008年)はうるう年ですので、366日として計算する必要があります。
とはいうものの、答えはやはり17人になるかと思います。
きゃすたさん
ご指摘の通りです!申し訳ありません。
初め、高校入学との問題を作成いたいまして、クラス数少なすぎるな...と中学入学に問題を訂正したのが、今回のミスでした...。
しっかり閏年を外す予定の問題だったんです...。
ありがとうございます。
ご指摘の通りです!申し訳ありません。
初め、高校入学との問題を作成いたいまして、クラス数少なすぎるな...と中学入学に問題を訂正したのが、今回のミスでした...。
しっかり閏年を外す予定の問題だったんです...。
ありがとうございます。
コメントするには、ログインまたはメンバー登録(無料)が必要です。